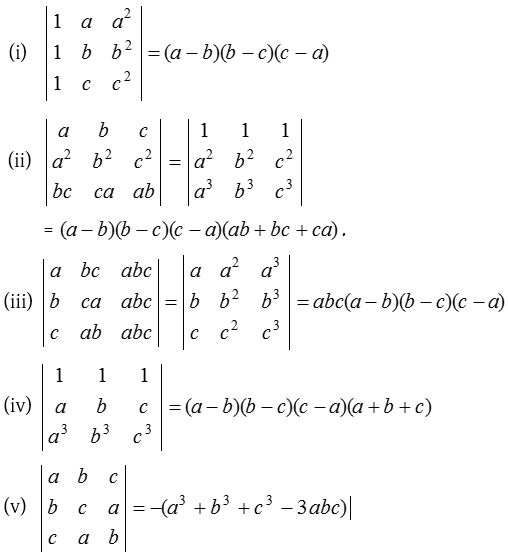Determinant of a Matrix

Determinant of a Matrix

Determinant

Let us consider three homogeneous linear equations a₁x + b₁y + c₁z = 0, a₂x + b₂y + c₂z = 0 and a₃x + b₃y + c₃z = 0
Eliminated x, y, z from above three equations we obtain
a₁(b₂c₃ − b₃c₂) − b₁(a₂c₃ –a₃c₂) + (a₂b₃ – a₃b₂) = 0 …….(i)

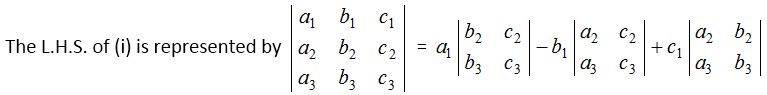
Its contains three rows and three columns, it is called a determinant of third order.
The number of elements in a second order is 2² = 4 and the number of elements in a third order determinant is 3² = 9.
Rows and columns of a determinant : In a determinant horizontal lines counting from top 1^st, 2^nd, 3^rd,….. respectively known as rows and denoted by R₁, R₂, R₃, ……. and vertical lines counting left to right, 1^st, 2^nd, 3^rd,….. respectively known as columns and denoted by C₁, C₂, C₃, …….

Properties of determinants

1. The value of determinant remains unchanged, if the rows and the columns are interchanged.
   Since the determinant remains unchanged when rows and columns are interchanged, it is obvious that any theorem which is true for ‘rows’ must also be true for ‘columns’.
2. If any two rows (or columns) of a determinant be interchanged, the determinant is unaltered in numerical value but is changed in sign only.
3. If a determinant has two rows (or columns) identical, then its value is zero.
4. If all the elements of any row (or column) be multiplied by the same number, then the value of determinant is multiplied by that number.
5. If each element of any row (or column) can be expressed as a sum of two terms, then the determinant can be expressed as the sum of the determinants.
   
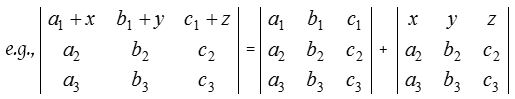
6. The value of a determinant is not altered by adding to the elements of any row (or column) the same multiples of the corresponding elements of any other row (or column)
   
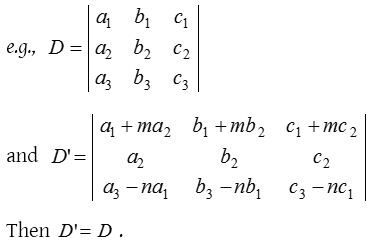
7. If all elements below leading diagonal or above leading diagonal or except leading diagonal elements are zero then the value of the determinant equal to multiplied of all leading diagonal elements.
8. If a determinant D becomes zero on putting x = α, then we say that x – α is factor of determinant.
9. It should be noted that while applying operations on determinants then at least one row (or column) must remain unchanged or, Maximum number of operations = order of determinant –1.
10. It should be noted that if the row (or column) which is changed by multiplied a non-zero number, then the determinant will be divided by that number.

Minors and Cofactors

Minor of an element:
If we take the element of the determinant and delete (remove) the row and column containing that element, the determinant left is called the minor of that element. It is denoted by M_ij.

Similarly, we can find the minors of other elements. Using this concept the value of determinant can be
∆ = a₁₁M₁₁ – a₁₂M₁₂ + a₁₃M₁₃
or, ∆ = – a₂₁M₂₁ + a₂₂M₂₂ – a₂₃M₂₃
or, ∆ = a₃₁M₃₁ – a₃₂M₃₂ + a₃₃M₃₃

Cofactor of an element:
The cofactor of an element a_ij (i.e. the element in the i^th row and j^th column) is defined as (–1)^i+j times the minor of that element. It is denoted by C_ij or A_{ij or} F_ij.
C_ij = (–1)^i+j M_ij.

where C₁₁ = (–1)¹⁺¹ M₁₁ = +M₁₁ , C₁₂ = (–1)¹⁺² M₁₂ = –M₁₂ and C₁₃ = (–1)¹⁺³ M₁₃ = +M₁₃
Similarly, we can find the cofactors of other elements.

Product of two determinants

Let the two determinants of third order be,

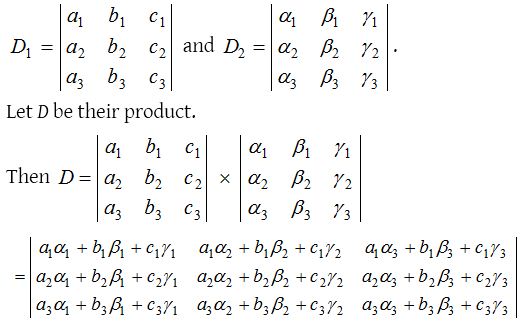
We can also multiply rows by columns or columns by rows or columns by columns.

Application of determinants in solving a system of linear equations

(1) Solution of system of linear equations in three variables by Cramer’s rule:
The solution of the system of linear equations
a₁x + b₁y + c₁z = d₁ …..(i)
a₂x + b₂y + c₂z = d₂  …..(ii)
a₃x + b₃y + c₃z = d₃  …..(iii)

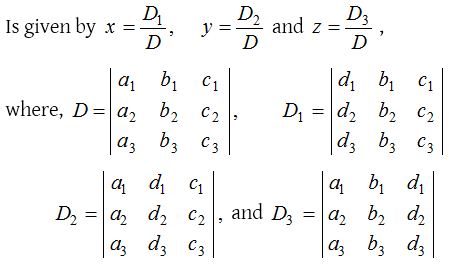
Provided that D ≠ 0
(2) Conditions for consistency:
For a system of 3 simultaneous linear equations in three unknown variable.
(i) If D ≠ 0, then the given system of equations is consistent and has a unique solution given by x = D₁/D, y = D₂/D and z = D₃/D.
(ii) If D = 0 and D₁ = D₂ = D₃ = 0, then the given system of equations is consistent with infinitely many solutions.
(iii) If D = 0 and at least one of the determinants D₁, D₂, D₃ is non-zero, then given of equations is inconsistent.

Some special determinants

(1) Symmetric determinant:
A determinant is called symmetric determinant if for its every element a_ij = – a_ji ∀ i, j.

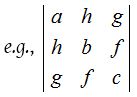
(2) Skew-symmetric determinant:
A determinant is called skew symmetric determinant if for its every element a_ij = – a_ji ∀ i, j.

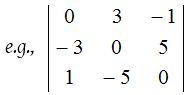
• Every diagonal element of a skew symmetric determinant is always zero.
• The value of a skew symmetric determinant of even order is always a perfect square and that of odd order is always zero.

(3) Cyclic order:
If elements of the rows (or columns) are in cyclic order. i.e.,