Derivative Rules

Derivative Rules

The rate of change of one quantity with respect to some another quantity has a great importance.
The rate of change of a quantity ‘y’ with respect to another quantity ‘x’ is called the derivative or differential coefficient of y with respect to x.

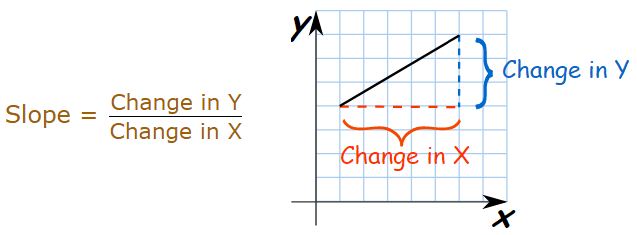
The Derivative means the slope of a function at any point.

Some Standard Differentiation Formulae

(1) Differentiation of some common functions:

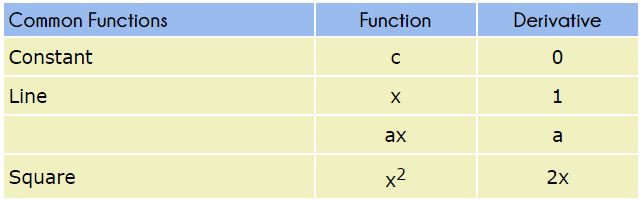
(2) Differentiation of algebraic functions:
In particular

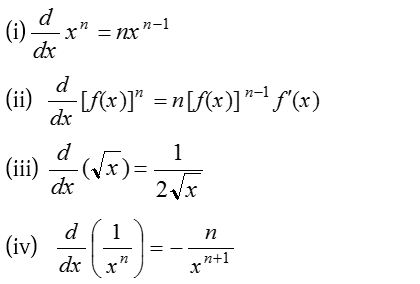
(3) Differentiation of trigonometric functions:

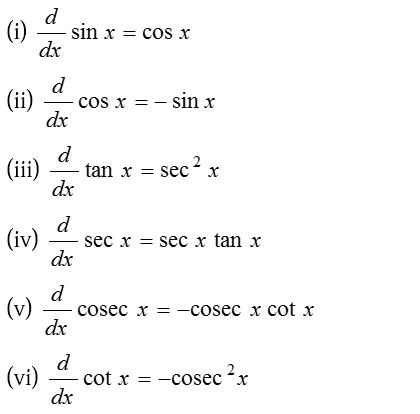
(4) Differentiation of logarithmic and exponential functions:

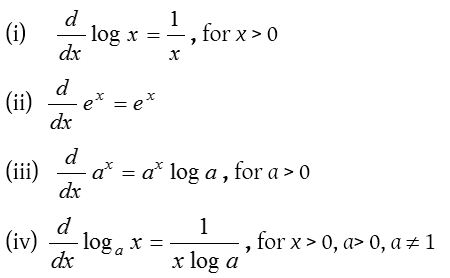
(5) Differentiation of inverse trigonometrical functions:

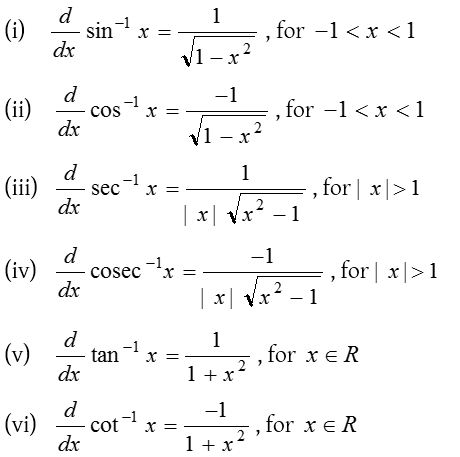
(6) Differentiation of hyperbolic functions:

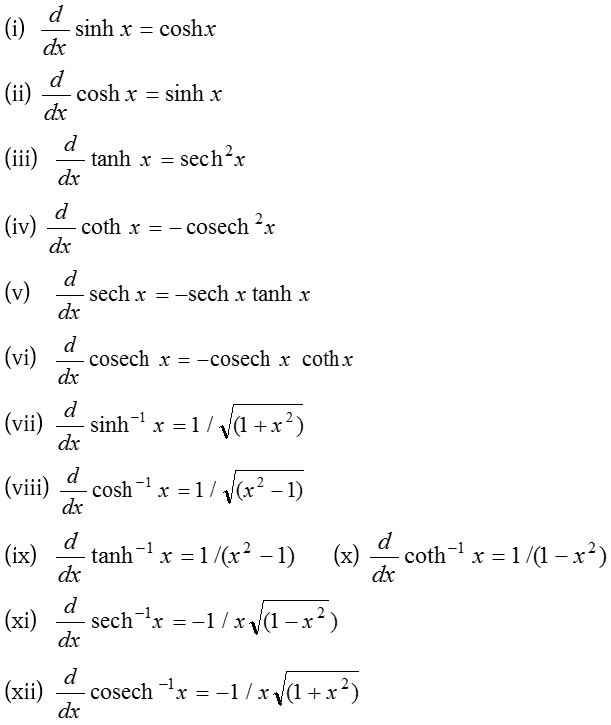
(7) Suitable substitutions

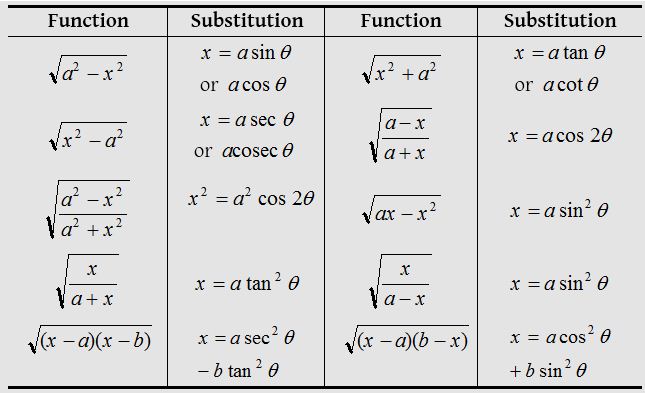
Rules for Differentiation

Let f(x), g(x) and u(x) be differentiable functions

1. If at all points of a certain interval, f'(x) = o, then the function f(x) has a constant value within this interval.
2. Chain rule
   (i) Case I: if y is a function of u and u is a function of x, then derivative of y with respect to x is
   
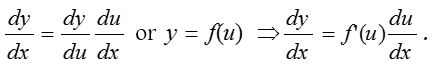
   (ii) Case II: If y and x both are expressed in terms of t, y and x both are differentiable with respect to t, then
   
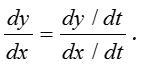
3. Sum and difference rule: Using linear property
   
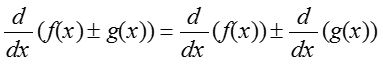
4. Product rule
   
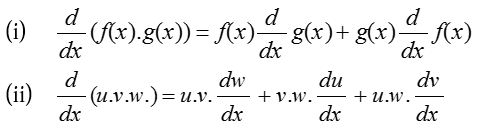
5. Scalar multiple rule:
   
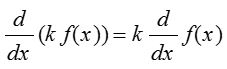
6. Quotient rule:
   
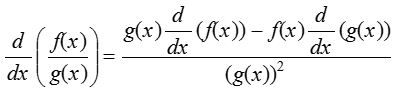
   Provided g≠0.