What is the meaning of Classmark and Prepare a Discrete Frequency Distribution
Important Points
- The word data means information. Statistical data are of two types :
(i) Primary data
(ii) Secondary data - When an investigator collects data himself with a definite plan or design in his (her) mind, it is called Primary data.
- Data which are not originally collected rather obtained from published or unpublished sources are known as Secondary data.
- After collection of data, the investigator has to find ways to condense them in tabular form in order to study their salient features. Such an arrangement is called Presentation of data.
- Raw data (if the data is arranged in the manner as it was collected, then it is called as Raw data) when put in ascending or descending order of magnitude is called an array or arranged data.
- The number of times an observation occurs in the given data is called frequency of the observation
Classes/class intervals are the groups in which all the observations are divided. - Suppose class-interval is 10-20, then 10 is called lower limit and 20 is called upper limit of the class.
- Mid-value of class-interval is called Class-mark.
Class-mark = \(\frac { Lower\quad limit+Upper\quad limit }{ 2 } \)
Class-mark = lower limit + \(\frac { 1 }{ 2 } \)
(difference between the upper and lower limits) - If the frequency of first class interval is added to the frequency of second class and this sum is added to third class and so on then frequencies so obtained are known as Cumulative Frequency (c.f.).
- There are two types of cumulative frequencies (a) less than, (b) greater than.
Read More:
- Cumulative Frequency in statistics
- How are Bar Graphs and Histograms Related
- Mean and its Advantages and Disadvantages
- Median of Grouped Frequency Distribution
- Mode in Statistics
- Pie Charts
- Frequency Polygon
- Bar Graph in Statistics
- RS Aggarwal Class 10 Solutions Mean, Median, Mode of Grouped Data
- RS Aggarwal Class 9 Solutions Statistics
Discrete Frequency Distribution Example Problems with Solutions
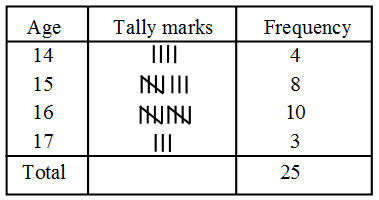
Example 1: Given below are the ages of 25 students of class IX in a school. Prepare a discrete frequency distribution.
15, 16, 16, 14, 17, 17, 16, 15, 15, 16, 16, 17, 15, 16, 16, 14, 16, 15, 14, 15, 16, 16, 15, 14, 15.
Solution: Frequency distribution of ages of 25 students
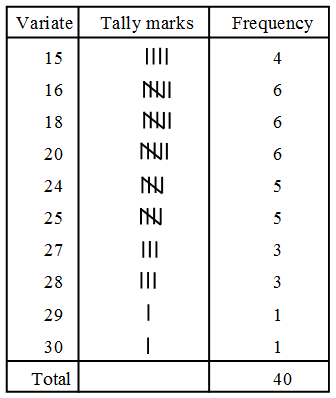
Example 2: Form a discrete frequency distribution from the following scores:-
15, 18, 16, 20, 25, 24, 25, 20, 16, 15, 18, 18, 16, 24, 15, 20, 28, 30, 27, 16, 24, 25, 20, 18, 28, 27, 25, 24, 24, 18, 18, 25, 20, 16, 15, 20, 27, 28, 29, 16.
Solution:
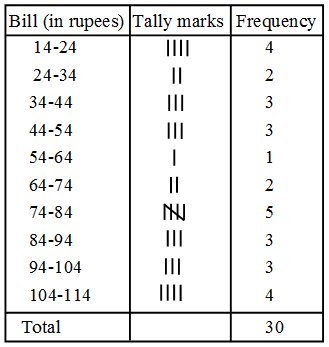
Example 3: The water tax bills (in rupees) of 30 houses in a locality are given below. Construct a grouped frequency distribution with class size of 10.
30, 32, 45, 54, 74, 78, 108, 112, 66, 76, 88, 40, 14, 20, 15, 35, 44, 66, 75, 84, 95, 96, 102, 110, 88, 74, 112, 14, 34, 44.
Solution: Here the maximum and minimum values of the variate are 112 and 14 respectively.
∴ Range = 112 – 14 = 98.
It is given that the class size is 10, and
\(\frac { Range }{ Class\quad size } =\frac { 98 }{ 10 } \) = 9.8
So, we should have 10 classes each of size 10. If we take the first class as 14-24 it includes the minimum value 14. If the last class is taken as 104-114, then it includes the maximum value 112. In the class 14-24, 14 is included but 24 is excluded. Similarly, in other classes, the lower limit is included and the upper limit is excluded. Now
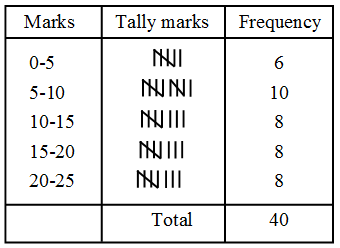
Example 4: The marks obtained by 40 students of class IX in an examination are given below :
18, 8, 12, 6, 8, 16, 12, 5, 23, 2,16, 23, 2, 10, 20, 12, 9, 7, 6, 5, 3, 5, 13, 21, 13, 15, 20, 24, 1, 7, 21, 16, 13, 18, 23, 7, 3, 18, 17, 16.
Present the data in the form of a frequency distribution using the same class size, one such class being 15-20 (where 20 is not included)
Solution: Frequency Distribution of Marks
Example 5: The class marks of a distribution are :
47, 52, 57, 62, 67, 72, 77, 82, 87, 92, 97, 102 Determine the class size, the class limits and the true class limits.
Solution: Here the class marks are uniformly spaced. So, the class size is the difference between any two consecutive class marks
∴ Class size = 52 – 47 = 5
We know that, if a is the class mark of a class interval and h is its class size, then the lower and upper limits of the class interval are
\(a-\frac { h }{ 2 } \) and \(a+\frac { h }{ 2 } \) respectively.
∴ Lower limit of first class interval
= \(47-\frac { 5 }{ 2 } \)
= 44.5
And, upper limit of first class interval
= \(47+\frac { 5 }{ 2 } \)
= 49.5
So, first class interval is 44.5 – 49.5
Similarly, we obtain the other class limits as given under :
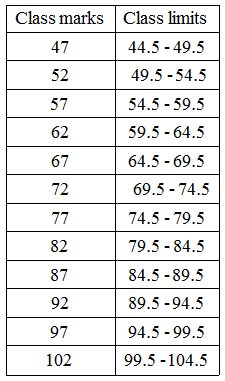 Since the classes are exclusive, so the true class limits are same as the class limits.
Since the classes are exclusive, so the true class limits are same as the class limits.
Example 6: The class marks of a distribution are 26, 31, 36, 41, 46, 51, 56, 61, 66, 71. Find the true class limits.
Solution: Here the class marks are uniformly spaced. So, the class size is the difference between any two consecutive class marks.
∴ Class size = 31 – 26 = 5.
If a is the class mark of a class interval of size h, then the lower and upper limits of the class interval are \(a-\frac { h }{ 2 } \) and \(a+\frac { h }{ 2 } \) respectively.
Here h = 5
∴ Lower limit of first class interval
= \(26-\frac { 5 }{ 2 } \) = 23.5
And, upper limit of first class interval
= \(26+\frac { 5 }{ 2 } \) = 28.5
∴ First class interval is 23.5 – 28.5.
Thus, the class intervals are:
23.5 – 28.5, 28.5 – 33.5, 33.5 – 38.5, 38.5 – 43.5, 43.5 – 48.5, 48.5 – 53.5
Since the class are formed by exclusive method. Therefore, these limits are true class limits.
Example 6: The class marks of a distribution are 82, 88, 94, 100, 106, 112 and 118. Determine the class size and the classes.
Solution: The class size is the difference between two consecutive class marks.
∴ Class size = 88 – 82 = 6.
Now 82 is the class mark of the first class whose width is 6.
∴ Class limits of the first class are \(82-\frac { 6 }{ 2 } \) and \(82+\frac { 6 }{ 2 } \) i.e. 79 and 85.
Thus, the first class is 79-85. Similarly, the other classes are 85–91, 91– 97, 97–103,
103 –109, 109 –115 and 115 –121.
Example 7: The class marks of a distribution are 13, 17, 21, 25 and 29. Find the true class limits.
Solution: The class marks are 13, 17, 21, 25 and 29.
The class marks are uniformly spaced.
Class size = difference between two consecutive class marks
= 17 – 13 = 4
Half of the class size = \(\frac { 4 }{ 2 } \) = 2
To find the classes one has to subtract 2 from and add 2 to each of the class marks.
Hence, the classes are
11– 15
15 – 19
19 – 23
23 – 27
27 – 31
Since the classes are exclusive, the true class limits are the same as the class limits. So the lower class limits as well as the true lower class limits are 11, 15, 19, 23 and 27. The upper class limits as well as the true upper class limits are 15, 19, 23, 27 and 31.
Example 8: Find the unknown entries (a,b,c,d,e,f,g) from the following frequency distribution of heights of 50 students in a class :
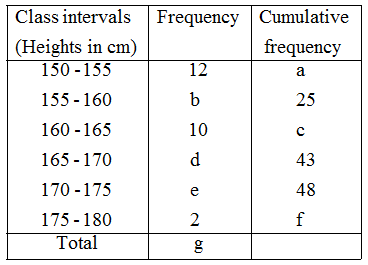
Solution: Since the given frequency distribution is the frequency distribution of heights of 50 students. Therefore,
∴ g = 50.
From the table, we have
a = 12, b + 12 = 25, 12 + b + 10 = c,
⇒ 12 + b + 10 + d = 43,
⇒ 12 + b + 10 + d + e = 48 and
⇒ 12 + b + 10 + d + e + 2 = f
Now, b + 12 = 25
⇒ b = 13
12 + b + 10 = c
⇒ 12 + 13 + 10 = c [∵ b = 13]
⇒ c = 35
12 + b + 10 + d = 43
⇒ 12 + 13 + 10 + d = 43 [∵ b = 13]
⇒ d = 8
12 + b + 10 + d + e = 48
⇒ 12 + 13 + 10 + 8 + e = 48 [∵ b = 13, d = 8]
⇒ e = 5
and, 12 + b + 10 + d + e + 2 = f
⇒ 12 + 13 + 10 + 8 + 5 + 2 = f
⇒ f = 50.
Hence, a = 12, b = 13, c = 35, d = 8,
e = 5, f = 50 and g = 50.
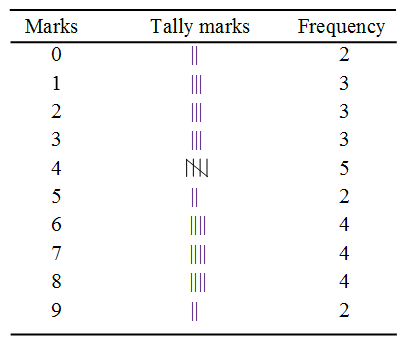
Example 9: The marks out of 10 obtained by 32 students are : 2, 4, 3, 1, 5, 4, 3, 8, 9, 7, 8, 5, 4, 3, 6, 7, 4, 7, 9, 8, 6, 4, 2, 1, 0, 0, 2, 6, 7, 8, 6, 1.
Array the data and form the frequency distribution
Solution: An array of the given data is prepared by arranging the scores in ascending order as follows :
0, 0, 1, 1, 1, 2, 2, 2, 3,3,3, 4,4,4,4,4,
5,5, 6,6,6,6, 7,7,7,7, 8,8,8,8, 9,9.
Frequency distribution of the marks is shown below.
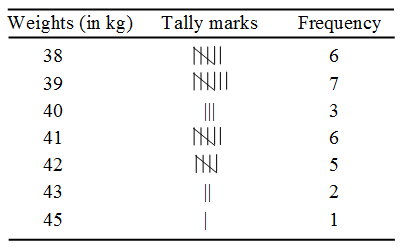
Example 10: Prepare a discrete frequency distribution from the data given below, showing the weights in kg of 30 students of class VI.
39, 38, 42, 41, 39, 38, 39, 42, 41, 39, 38, 38 41, 40, 41, 42, 41, 39, 40, 38, 42, 43, 45, 43, 39, 38, 41, 40, 42, 39.
Solution: The discrete frequency distribution table for the weight (in kg) of 30 students is shown below.