CBSE Sample Papers for Class 12 Maths Paper 5 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 5.
CBSE Sample Papers for Class 12 Maths Paper 5
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 5 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 5 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
Cartesian equation of a line PQ is \(\frac { 2x-1 }{ 2 } =\frac { 4-y }{ 6 } =\frac { z+1 }{ 7 }\). Write the direction ratios of a line parallel to PQ.
Question 2.
Find an antiderivative of (ax + b)2 by the method of inspection.
Question 3.
Check the continuity of the function
Question 4.
Find the value of \(\begin{vmatrix} { cos45 }^{ 0 } & { sin90 }^{ 0 } \\ { -sin45 }^{ 0 } & { cos90 }^{ 0 } \end{vmatrix}\)
SECTION B
Question 5.
Find the matrix A, satisfying the matrix equation
Question 6.
Find the derivative of log [log (log x5)] w.r.t. x.
Question 7.
In a competition a brave child tries to inflate a huge spherical balloon at the rate of 1000 cm3/sec. Find the rate at which the radius of the balloon is increasing when its radius is 15 cm.
Question 8.
If the function f(x) is differentiable at x = 2, then find the value of a and b.
Question 9.
Find the vector and the cartesian equation of the line that passes through the origin and (5, -2, 3).
Question 10.
If P(A) = 0.8, P(B) = 0.5, P(B|A) = 0.4, then find P(A ∪ B).
Question 11.
One kind of cake requires 200 gm of flour and 25 gm of fat and another kind of cake requires 100 gm of flour and 50 gm of fat. Make an LPP to find the maximum number of cakes made from 5 kg of flour and 1 kg of fat.
Question 12.
Evaluate \(\int _{ 0 }^{ 2 }{ { \left[ x \right] }^{ 2 } } dx\)
SECTION C
Question 13.
Question 14.

Question 15.
Differentiate (xcosx)x + (xsinx)1/x w.r.t. x.
Question 16.
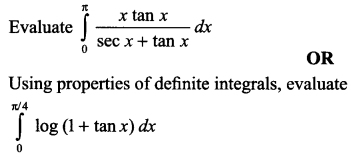
Question 17.
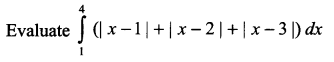
Question 18.
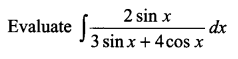
Question 19.
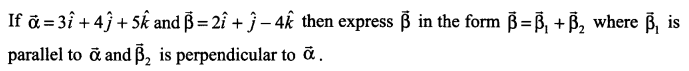
Question 20.
Question 21.
Two persons A and B thrown die alternately till one of them gets a ‘three’ and wins the game. Find their respective probability of winning if A begins.
Question 22.
12 cards numbered 1 to 12 are placed in a box, mixed up thoroughly and then a card is drawn at random from the box. If it is known that the number on the drawn card is more than 3, find the probability that it is an even number. Write any two values which are reflected in the bright students, report card?
Question 23.
Solve the following L.P.P. graphically.
Maximise profit Z = ₹ (80x + 120y)
Subject to constraints are
9x + 12y ≤ 180
1x + 3y ≤ 30
x, y ≥ 0
SECTION D
Question 24.
Let L be the set of all lines in the XY plane and R be the relation on L defined as R = {(L1, L2) : L1 is parallel to L2}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.
OR
Let * be the binary operation on N given by a * b = LCM of a and b. Find
(i) 5 * 7
(if) 20 * 16
(Hi) Is * commutative?
(iv) Is * associative?
(v) Find the identity of * in N.
(vi) Which element of N is invertible for operation * ?
Question 25.
Using the method of integration find the area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x.
OR
Question 26.
Show that the general solution of the differential equation \(\frac { dy }{ dx } +\frac { { y }^{ 2 }+y+1 }{ { x }^{ 2 }+x+1 } =0\) is given by (x + y + 1) = A (1 – x – y – 2xy) where A is a parameter.
Question 27.
Find the length and the foot of the perpendicular from the point P(7, 14, 5) to the plane 2x + 4y – z = 2. Also find the image of point P in the plane.
OR
A line makes an angle α, β, γ, δ with four diagonals of a cube prove that \({ cos }^{ 2 }\alpha +{ cos }^{ 2 }\beta +{ cos }^{ 2 }\gamma +{ cos }^{ 2 }\delta =\frac { 4 }{ 3 }\)
Question 28.
The cost of 4 kg onion, 3 kg wheat and 2 kg rice is ₹ 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is ₹ 90. The cost of 6 kg onion, 2 kg wheat and 3 kg rice is ₹ 70. Find the cost of each item per kg by matrix method.
Question 29.
A helicopter is flying along the curve y = x2 + 2. A soldier is placed at the point (3, 2). Find the nearest distance between the
soldier and the helicopter.
Solutions
Solution 1.
Direction ratio of a line parallel to PQ are 1, -6, 7
Solution 2.
\(\frac { 1 }{ 3a }\) (ax + b)3
Solution 3.
Here L.H.L ≠ R.H.L, so f(x) is not continuous at x = 0
Solution 4.
Solution 5.
Solution 6.
Solution 7.
Solution 8.
f(x) is differentiable at x = 2, so it is also continuous at x = 2
L.H.L = 4
R.H.L = 2a + b
2a + b = 4 …….(2)
From (1) and (2),
a = 4, b = -4
Solution 9.

Solution 10.
P(A ∩B) = P(A) P(B|A) = 0.32
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0.98
Solution 11.
Let x number of cakes of one kind and number of cakes of other kind.
Objective function is maximise Z = x + y
Subject to constraints are
200x + 100y ≤ 5000
25x + 50y ≤ 1000
x, y ≥ 0
Solution 12.
Solution 13.

Solution 14.
C1 → C1 + C2 + C3
Taking (a + x + y + z) common
After this R1 → R1 – R2, R2 → R2 – R3 and expand
OR
C1 → C1 + C2 + C3
Taking (5x + λ) common
After this R1 → R1 – R2, R2 → R2 – R3 and expand
Solution 15.
Solution 16.
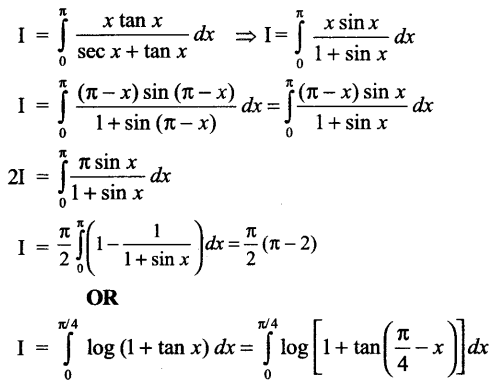
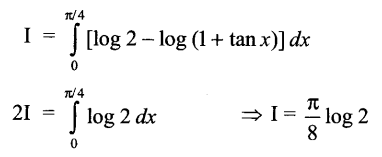
Solution 17.
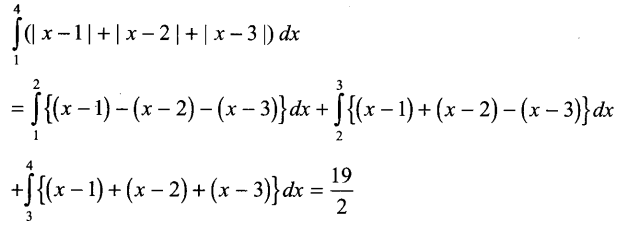
Solution 18.
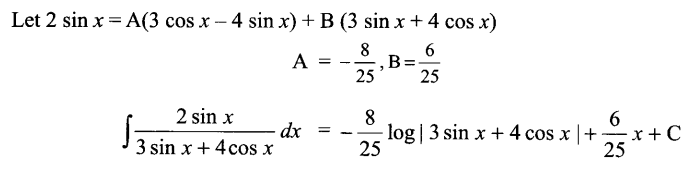
Solution 19.
Solution 20.
Solution 21.
Let E : person A gets three
F : person B gets three
Solution 22.
E : Number on the card drawn is even
F : Number on the card drawn is more than 3.
E = {2, 4, 6, 8, 10, 12}, F = {4, 5, 6, 7, 8, 9, 10, 11, 12}
E ∩ F = {4, 6, 8, 10, 12}
Values in report card: Good performance through marks and punctuality through attendance.
Solution 23.
Solution 24.
Prove it is reflexive, Prove it is symmetric, Prove it is transitive.
Because it is reflexive, symmetric and transitive, so it is an equivalence relation.
Set of lines related to the line y = 2x + 4 is y = 2x + k where k is any real number.
OR
(i) 5 * 7 = 35
(ii) 20 * 16 = 80
(iii) Prove * is commutative
(iv) Prove * is associative
(v) Identity of * in N = 1
(vi) Only the element 1 in N is invertible for the operation * because 1 * 1 = 1
Solution 25.
Solution 26.
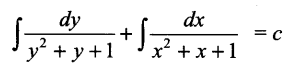
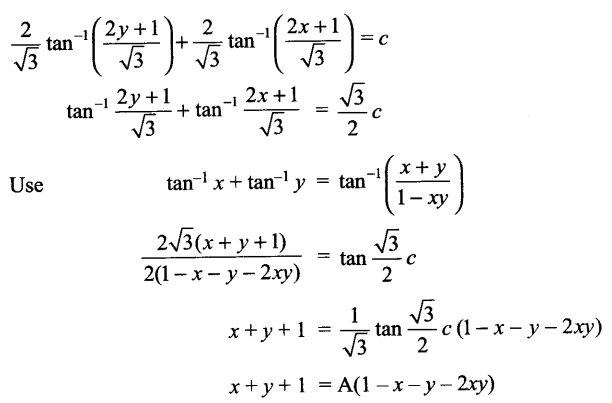
Solution 27.

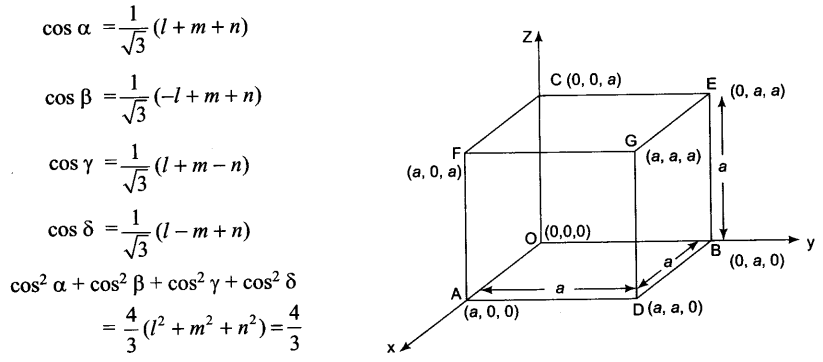
Solution 28.
Let price of 1 kg onion = ₹ x
Price of 1 kg wheat = ₹ y
Price of 1 kg rice = ₹ z
4x + 3y + 2z = 60
2x + 4y + 6z = 90
6x + 2y + 3z = 70

Solution 29.
Let P(x, y) be the position of helicopter and Q (3, 2) is of soldier

We hope the CBSE Sample Papers for Class 12 Maths Paper 5 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 5, drop a comment below and we will get back to you at the earliest.