Understanding Pressure in Liquids
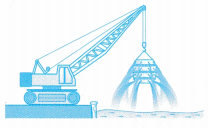
Figure shows an old container being hoisted from the sea. The water in the container flows out in all directions. This is because pressure in a liquid acts in all directions.
The man in Figure is not going to the outer space. Fie is actually a deep-sea diver wearing a magnesium alloy suit which can withstand high underwater pressure. This is because pressure in a liquid increases with depth.

Formula for Pressure in Liquids

- The pressure, P of a liquid at a particular depth in the liquid is given by the formula:
P = hρg
where h is the depth, ρ is the “density of the liquid and g is the gravitational field strength.

- Pressure exerted by the liquid is the same in all directions about a point.
- Pressure exerted is the same at all points in a horizontal plane as well as in a stationary liquid.
Applications of Pressure in Liquids
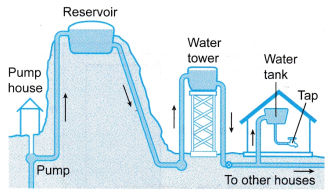
- Figure shows a simple system of how water flows to the taps in your house. The reservoir, water tower and water tank are placed high above the ground so that a high pressure difference is maintained for water to flow. Without this pressure difference, water would not flow.
- Figure shows a hydroelectric power station. The dam raises the water level in the reservoir so that it is much higher than the turbine of the generator. As a result, water flows into the turbine at a very high pressure and turns the turbine to generate electricity.

- Figure shows a patient being put on a drip. The nutrient bottle is hung on a pole so that it is higher than the end of the tube attached to the intravenous needle on the patient’s hand. This makes the pressure of the nutrient solution at the end of the tube greater than the blood pressure of the vein in the patient’s hand. As a result, the nutrient solution is able to flow into the vein.

Ways to Reduce the Negative Effects of Pressure in Liquids
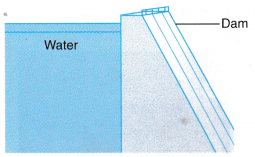
- Figure shows a dam retaining water in a reservoir. The dam must be able to withstand the force exerted against it by the water it retains. Since this pressure increases with the depth of the water, the base of the dam is broader in order to withstand a bigger force.
- Specially constructed vehicles known as submersibles, as shown in Figure, are used to transport people in the deep sea. The body of these submersibles can withstand the tremendously high pressure due to the great depth of the sea.

- A diver venturing into deep sea will not be able to breathe properly using ordinary scuba diving equipment because the high water pressure exerted on his body prevents his lungs from expanding. The diver will have to wear an all encasing suit, as shown in Figure, and move around with the help of a propeller attached to the suit.

- Sometimes unmanned remotely operated vehicles are used for deep-sea exploration. These vehicles are actually robots that can carry out various underwater tasks like pipeline repairs, seabed mapping, exploration and researches. The bodies of these vehicles must be able to withstand tremendous amounts of water pressure without collapsing.
Activity
Aim: To study factors affecting the pressure in a liquid.
Materials: Water, alcohol, glycerine, a thin rubber sheet
Apparatus: Manometer filled with coloured paraffin, rubber tube, thistle funnel, tall plastic bottle, metre rule, retort stand with clamp, rubber band
A. Relationship between Depth and Pressure in a Liquid
Method:
- The apparatus is arranged as shown in Figure.

- The thistle funnel is lowered into the water at different depths of h.
- The corresponding readings for l from the manometer are measured and recorded.
Observation:
It is observed that when the value of h is increased, the value of l increases.
Discussion:
- The values of l are an indicator for the pressure of water at various depths of h. The bigger the value of l, the higher is the pressure of the water measured.
- Hence, from the above activity, we can conclude that the pressure of the water increases with depth.
- Generally, the pressure in a liquid increases with depth.
B. Relationship between Density and Pressure in a Liquid
Method:
The above activity is repeated by replacing water with alcohol (density 800 kg m-3) and then, with glycerine (density 1300 kg m-3).
Observation:
It is observed that for a fixed value of h, the values of l is biggest for glycerine followed by water and then alcohol.
Discussion:
- When we fix the value of h, we are making the depth a fixed variable.
- We manipulate the density of the liquid by using liquids of different density.
- (a) Let ρglycerine , ρwater and ρalcohol represent the density of glycerine, water and alcohol respectively. Also, let lglycerine , lwater and lalcohol represent the manometer readings for glycerine, water and alcohol respectively.
(b) Given that ρglycerine > ρwater > ρalcohol and from the observation lglycerine > lwater > lalcohol we can conclude that the pressure of the liquid increases with density. - Generally, the pressure in a liquid increases with density.
Conclusion:
1. The pressure in a liquid increases with depth.
2. The pressure in a liquid increases with density.
Pressure in Liquids Example Problems with Solutions
Example 1. What will be the pressure in N/m2 at a depth of 1.5 m in brine of density 120 kg/cm3 ?
Solution: P = hρg
=15 × 120 × 10
= 1800 N/m2
Example 2. Calculate the density of a liquid if the pressure at a point 30 m below its surface is 32 × 104 N/m2.
Solution: P = hρg
\( \Rightarrow d=\frac{P}{hg} \)
\( =\frac{32\times {{10}^{4}}}{30\times 10}=1066.6\text{ kg/}{{\text{m}}^{3}} \)
Example 3. Figure shows a submarine travelling from the surface of the sea to a depth of 6000 m.

If the density of sea water is 1025 kg m-3 and by taking g = 9.8 N kg-1, calculate the pressure exerted by the sea water on the submarine at that depth.
Solution:
Using the formula P = hρg,
P = 6000 x 1025 x 9.8
= 6.03 x 107 Pa
Example 4. Figure shows a farmer’s ingenious method of drawing water from a pond located at a nearby hill by using a metal pipe. Water rushing out of the holes at the lower end of the pipe irrigates his plants.

Calculate the pressure of the water rushing out of the holes. [Density of water = 103 kg m-3; g = 9.8 N kg-1]
Solution:
Pressure of water rushing out of the holes,
P = hρg = 16 x 103 x 9.8
= 1.57 x 105 Pa
Example 5. Calculate the pressure exerted by the water retained by a dam at a depth of 60 m.
[Density of water = 1000 kg m-3; g = 9.8 N kg-1]
Solution:
Using formula P = hρg
P = 60 x 1000 x 9.8
= 5.88 x 105 Pa
Example 6. A scientist has invented a robot to work at the seabed. According to his calculation, the armour of the robot can withstand a maximum pressure of 106 Pa exerted by the sea water. If the density of sea water is 1025 kg m-3 and g = 9.8 N kg-1, what is the maximum depth of the seabed that this robot can work at?
Solution:
