How do you find the Surface Area and Volume of a Cube
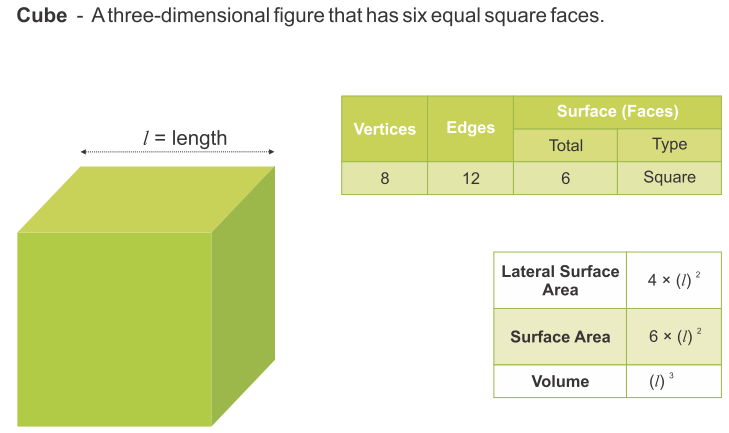
If the length of each edge of a cube is ‘a’ units, then
- Total surface area of the cube = 6a2 sq. units.
- Lateral surface area = 4a2
- Volume of the cube = a3 cubic units
- Diagonal of the cube = a units.
- Length of its diagonals = a√3
- Total length of its edges = 12a
Read More:
Surface Area and Volume of a Cube Example Problems with Solutions
Example 1: If each edge (side) of a cube is 8 cm ; find its surface area and lateral surface area.
Solution: Given each side of the cube (a) = 8 cm
∴ Its surface area = 6a2 = 6 × 82 sq. cm
= 6 × 64 cm2 = 384 cm2
Lateral surface area = 4a2 = 4 × 82 sq. cm
= 4 × 64 cm2 = 256 cm2
Example 2: A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much ?
(ii) Which box has the smaller total surface area and by how much ?
Solution: (i) For the cubical box :
Each edge = 10 cm i.e., a = 10 cm
∴ Lateral surface area of the cubical box
= 4a2 = 4 × 102 cm2 = 400 cm2
For the cuboidal box :
ℓ = 12.5 cm, b = 10 cm & h = 8 cm
∴ Lateral surface area of the cuboidal box
= 2(ℓ + b) × h
= 2(12.5 + 10) × 8 cm2
= 2 × 22.5 × 8 cm2 = 360 cm2
Clearly, cubical box has greater lateral surface area by
400 cm2 – 360 cm2 = 40 cm2
(ii) Total surface area of the cubical box:
= 6 a2 = 6 × 102 sq. cm = 600 cm2
Total surface area of the cuboidal box
= 2(ℓ × b + b × h + h × ℓ)
= 2(12.5 × 10 +10 × 8 + 8 × 12.5) cm2 = 2(125 + 80 + 100) cm2 = 610 cm2
Clearly, cubical box has smaller surface area by
610 cm2 – 600 cm2 = 10 cm2
Example 3: Find the volume of a solid cube of side 12 cm. If this cube is cut into 8 identical cubes, find :
(i) Volume of each small cube.
(ii) Side of each small cube.
(iii) Surface area of each small cube.
Solution: Since, side (edge) of the given solid cube = 12 cm.
∴ Volume of given solid cube = (edge)3
= (12 cm)3 = 1728 cm3 Ans.
(i) As the given cube is cut into 8 identical cubes.
⇒ Vol. of 8 small cubes obtained
= Vol. of given cube = 1728 cm3
⇒ Volume of each small cube
= \(\frac{{1728\,\,c{m^3}}}{8}\) = 216 cm3
(ii) If edge (side) of each small cube = x cm
(edge)3 = Volume
⇒ x3 = 216 = 6 × 6 × 6 = 63 ⇒ x = 6 cm
∴ Side of each small cube = 6 cm
(iii) Surface area of each small cube
= 6 × (edge)2
= 6 × (6 cm)2 = 216 cm2
Example 4: A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute ?
Solution: Volume of water that flows through a river, canal or pipe, etc., in unit time
= Area of cross-section × Speed of water through it.
x km/hr = x × \(\frac{5}{{18}}m/s\)
Reason : 1 km/hr = \(\frac{{1000m}}{{60 \times 60\,\,\,\sec }} = \frac{5}{{18}}m/s\)
Since, area of cross-section of the river
= Its depth × its width
= 3m × 40m = 120 m2
And, speed of flow of water through the river
= 2 km/hr = 2 × \(\frac{5}{{18}}m/s = \frac{5}{9}m/s\)
∴ Vol. of water that flows through it in 1 sec.
= Area of cross-section × speed of water through it.
= 120 × \(\frac{5}{9}{m^3} = \frac{{200}}{3}{m^3}\)
⇒ Vol. of water that flows through it in
1 min. (60 sec.)
= \(\frac{{200}}{3} \times 60\,\,{m^3}\) = 4000 m3
⇒ Vol. of water that will fall into the sea in a minute. = 4000 m3
Example 5: The volume of a cube is numerically equal to its surface area. Find the length of its one side.
Solution: Let length of each side is a unit.
Given: Volume of the cube = Surface area of the cube.
⇒ a3 = 6a2 ⇒ a = 6
∴ The length of one side of the cube = 6 cm
Example 6: A solid cuboid has square base and height
12 cm. If its volume is 768 cm3, find :
(i) side of its square base.
(ii) surface area.
Solution: (i) Let side of the square base be x cm
i.e., ℓ = b = x cm
ℓ × b × h = volume
⇒ x × x × 12 = 768
[Given, height = 12 cm]
⇒ x2 = \(\frac{{768}}{{12}} = 64\) ⇒ x = √64cm = 8 cm.
∴ Side of the square base = 8 cm
(ii) Now, ℓ = 8 cm, b = 8 cm and h = 12 cm
∴ Surface area = 2(ℓ × b + b × h + h × ℓ)
= 2(8 × 8 + 8 × 12 + 12 × 8) cm2 = 512 cm2