How do you find the Surface Area of a Sphere and a Hemisphere

Let radius of sphere = r. Then
- Surface area of a sphere = 4πr2
- Curved surface area of a hemisphere = 2πr2
- Total surface area of a hemisphere = 3πr2
- Volume of the sphere = \(\frac{4}{3}\pi {r^3}\)
- Volume of the hemisphere = \(\frac{2}{3}\pi {r^3}\)
Read More:
Surface Area and Volume of a Cuboid
Surface Area and Volume of a Cube
Surface Area of a Sphere and a Hemisphere Example Problems with Solutions
Example 1: Find the total surface area of the hemisphere of radius 20 cm. (Take π = 3.14).
Solution: Total surface area of the hemisphere
= 3πr2
= 3 × 3.14 × (20)2 cm2
[Given : r = 20 cm]
= 3768 cm2
Example 2: The area of the flat surface of a hemisphere is 154 cm2. Find its total surface area.
Solution: Given : πr2 = 154
⇒ \(\frac{{22}}{7}{r^2} = 154\)
⇒ r2 = 154 × \(\frac{7}{{22}} = 49\)
⇒ r = 7 cm
∴ Its total surface are = 3pr2
= 3 × \(\frac{{22}}{7} \times 7 \times 7c{m^2} = 462\,c{m^2}\)
Alternative method :
Total surface area of the hemisphere = 3πr2
= 3 × 154 cm2 [Given : πr2 = 154]
= 462 cm2
Example 3: The radius of a spherical balloon increases from 10 cm to 15 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Solution: Required ratio
= \(\frac{{Surface\,\,area\,\,of\,\,the\,\,balloon\,\,in\,\,1st\,\,case}}{{Surface\,\,area\,\,of\,\,the\,\,balloon\,\,in\,\,2nd\,\,case}}\)
= \(\frac{{4\pi {r^2}\,\,in\,\,1st\,\,case}}{{4\pi {r^2}\,\,in\,\,2nd\,\,case}}\) = \(\frac{{4 \times \pi \times 10 \times 10}}{{4 \times \pi \times 15 \times 15}} = \frac{4}{9}\)
= 4 : 9
Example 4: A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin plating it on the inside at the rate of Rs. 16 per 100 cm2.
Solution: ∵ Inner diameter = 10.5 cm
⇒ Inner radius (r) = 5.25 cm
The area of tin plating = Inner curved surface area of the bowl = 2πr2
= 2 × \(\frac{22}{7}\) × 5.25 × 5.25 cm2
= 173.25 cm2
∵ Cost of 100 cm2 tin-plating = Rs.16
⇒ Cost of 1 cm2 tin-plating = \(\frac{16}{100}\)
⇒ Cost of 173.25 cm2 tin-plating
= Rs.\(\frac{{16}}{{100}} \times 173.25\) = Rs. 27.72
Example 5: A right circular cylinder just encloses a sphere of radius r (see the given figure.). Find:
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii).
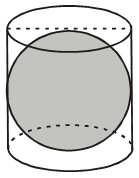
Solution: (i) Surface area of the sphere = 4πr2
(ii) Since, the height of the cylinder = diameter of the sphere
⇒ h = 2r ∴ C.S.A. of the cylinder
= 2πrh = 2πr × 2r = 4πr2
(iii) Required ratio = \(\frac{{4\pi {r^2}}}{{4\pi {r^2}}}\) = 1 = 1 : 1
If a cylinder just encloses a sphere, the surface area of the sphere is always same as the curved surface area of the cylinder.
In other words, if a sphere and a cylinder have the same radius and same height, there curved surface areas are also equal.
Example 6: Find the formula for the total surface area of each figure given bellow :

Solution: (i) Required surface area
= C.S.A. of the hemisphere + C.S.A. of the cone
= 2πr2 + πrℓ = πr (2r + ℓ)
(ii) Required surface area
= 2 × C.S.A. of a hemisphere + C.S.A. of the cylinder
= 2 × 2πr2 + 2πrh = 2πr (2r + h) .
(iii) Required surface area
= C.S.A. of the hemisphere + C.S.A. of the cylinder + C.S.A. of the cone
= 2πr2 + 2πrh + πrℓ = πr (2r + 2h + ℓ)
(iv) If slant height of the given cone be ℓ
= ℓ 2 = h2 + r2
⇒ ℓ = \(\sqrt {{h^2} + {r^2}}\)
And, required surface area
= 2πr2 + πrℓ = πr (2r + ℓ)
= πr\(\left( {2r + \sqrt {{h^2} + {r^2}} } \right)\)
Example 7: The radius of a sphere increases by 25%. Find the percentage increase in its surface area.
Solution: Let the original radius be r.
⇒ Original surface area of the sphere = 4πr2
Increase radius = r + 25% of r
= r + \(\frac{{25}}{{100}}r = \frac{{5r}}{4}\)
⇒ Increased surface area
= 4π\({\left( {\frac{{5r}}{4}} \right)^2} = \frac{{25\pi {r^2}}}{4}\)
Increased in surface area
= \(\frac{{25\pi {r^2}}}{4}–4\pi {r^2}\)
= \(\frac{{25\pi {r^2} – 16\pi {r^2}}}{4} = \frac{{9\pi {r^2}}}{4}\)
and, percentage increase in surface area
= \(\frac{{Increase\,\,in\,\,area}}{{Original\,\,aera}} \times 100\%\)
= \(\frac{{\frac{{9\pi {r^2}}}{4}}}{{4\pi {r^2}}} \times 100\% = \frac{9}{{16}}\)× 100%
= 56.25%
Alternative Method :
Let original radius = 100
⇒ Original C.S.A. = π(100)2 = 10000π
Increased radius = 100 + 25% of 100 = 125
⇒ Increased C.S.A. = π(125)2 = 15625π
Increase in C.S.S. = 15625π – 10000π
= 5625π
∴ Percentage increase in C.S.A.
= \(\frac{{Increase\,\,in\,\,C.S.A.}}{{Original\,C.S.A}} \times 100\%\)
= \(\frac{{5625\pi }}{{1000\pi }} \times 100\%\) = 56.25%
If the radius increases by 25%, the diameter also increases by 25%.
Conversely, if diameter decreases by 20%, the radius also decreases by 20%.
Example 8: The diameter of a solid metallic ball is 8.4 cm. Find its mass, if density of its material is 6.8 gm per cm3.
Solution: Since, diameter of the ball = 8.4 cm,
its radius (r) = \(\frac{{8.4}}{2}cm\) = 4.2 cm
Volume of material in the ball
= Volume of the ball = \(\frac{4}{3}\pi {r^3}\)
= \(\frac{4}{3} \times \frac{{22}}{7}\) × 4.2 × 4.2 × 4.2 cm3 = 310.464 cm3
Since, mass = Volume × density
∴ Mass of the ball
= 310.464 × 6.8 gm
= 2111.1552 gm = 2.111 kg (App.)
Example 9: The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon ?
Solution: Given : The diameter of the moon
= \(\frac{1}{4}\) × the diameter of the earth
⇒ The radius of the moon
= \(\frac{1}{4}\) × the radius of the earth.
⇒ Rm = \(\frac{1}{4}\) × Re
Now,
= \(\frac{{the\,volume\,of\,the\,moon}}{{the\,volume\,of\,the\,earth}} = \frac{{\frac{4}{3}\pi R_m^3}}{{\frac{4}{3}\pi R_e^3}}\)
= \(\frac{{R_m^3}}{{R_e^3}} = \frac{{{{\left( {\frac{1}{4}{R_e}} \right)}^3}}}{{R_e^3}} = \frac{1}{{64}}\)
∴ The volume of the moon
= \(\frac{1}{64}\) times the volume of earth.
Example 10: Twenty seven solid iron spheres, each of radius r and surface area S, are melted to form a sphere with surface area S’. Find the-
(i) radius r’ of the new sphere,
(ii) ratio of S and S’.
Solution: (i) Vol. of bigger solid sphere formed
= 24 × vol. of each solid sphere melted.
⇒ \(\frac{4}{3}\pi {(r’)^3} = 27 \times \frac{4}{3}\pi {r^3}\)
⇒ (r’)3 = 27r3 = (3r)3 ⇒ r’ = 3r
(ii) ∵ S = surface area of each sphere melted = 4πr2
And, S’ = Surface area of the sphere formed
= 4π(r’)2 = 4π(3r)2 = 36πr2
∴ Ratio of S and S’ = \(\frac{S}{{S’}}\) = \(\frac{{4\pi {r^2}}}{{36\pi {r^2}}} = \frac{1}{9}\) = 1 : 9
Example 11: A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Solution: Since, the inner radius (r) = 1 m = 100 cm and thickness of sheet = 1cm
∴ External radius (R) = 100 cm + 1 cm = 101 cm
∴ The volume of the iron used to make the
hemispherical tank
= Its external volume – Its internal volume
= \(\frac{2}{3}\pi {R^3}–\frac{2}{3}\pi {r^3}\) = \(\frac{2}{3}\pi\)(R3 – r3)
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × (1013 – 1003) cm3 = 63487.81 cm3
Example 12: A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of Rs. 498.96. If the cost of white-washing is Rs. 2.00 per square meter, find the
(i) inside surface area of the dome,
(ii) volume of the air inside the dome.
Solution: (i) Cost of white-washing = Rate of white-washing × Surface area of the dome.
⇒ Rs. 498.96 = Rs. 2 × Surface area of the dome.
⇒ Surface area of the dome
= \(\frac{{498.96}}{2}{m^2}\) = 249.48 m2
(ii) Let radius of the hemispherical dome = r m
∴ 2πr2 = 249.48
⇒ 2 × \(\frac{{22}}{7} \times {r^2}\) = 249.48
⇒ r2 = \(\frac{{249.48 \times 7}}{{2 \times 22}}{m^2}\) = 39.69
⇒ r = 6.3 m.
∴ Volume of air inside the dome
= \(\frac{2}{3}\pi {r^3}\) = \(\frac{2}{3}\) × \(\frac{22}{7}\) × 6.3 × 6.3 × 6.3 m3
= 523.908 m3 .
Example 13: The radii of two spheres are in the ratio 3 : 2. Find the ratio between their volumes.
Solution: Given Ratio between the radii of two spheres = 3 : 2
⇒ If radius of one sphere = 3r,
radius of the other = 2r
Required ratio = \(\frac{{Volume\,\,of\,\,one\,\,sphere}}{{Volume\,\,of\,\,other\,\,sphere}}\)
\(\frac{{\frac{4}{3} \times \pi \times {{(3r)}^3}}}{{\frac{4}{3} \times \pi \times {{(2r)}^3}}} = \frac{{27}}{8}\) = 27 : 8
Example 14: Three solid spheres of radii 1 cm, 6 cm and 8 cm are melted and recasted into a single sphere. Find the radius of the sphere obtained.
Solution: Let radius of the sphere obtained = R cm.
∴ \(\frac{4}{3} \times \pi {R^3} = \frac{4}{3}\pi {(1)^3} + \frac{4}{3}\pi {(6)^3} + \frac{4}{3}\pi {(8)^3}\)
R3 = 1 + 216 + 512
R = (729)1/3
R = 9 cm.
Example 15: A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Find the internal diameter of the shell.
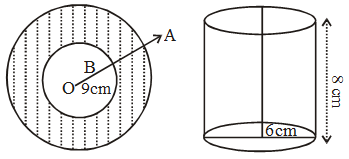
Solution: We have, height of the right circular cylinder = h = 8cm and radius of the base of it = R = 6cm
So, volume of it = πR2h = \(\left( {\frac{{22}}{7}\, \times \,6\, \times \,6\, \times \,8} \right)\) cm3 ….(i)
It is given that the external diameter of the spherical shell = 18 cm
⇒ The external radius of it = r1 = \(\frac{{18}}{2}\) = 9 cm
Let the internal radius of it be r2 cm.
Since the spherical shell is melted and recast into a right circular cylinder, we have the volume of the solid of spherical shell = volume of the cylinder
⇒ \(\frac{4}{3}\)π(r13 – r23) = \(\frac{22}{7}\) × 6 × 6× 8
[Using equation (i)]
⇒ \(\frac{4}{3}\) × \(\frac{22}{7}\)(93 – r23) = \(\frac{22}{7}\) × × 36 × 8
⇒ \(\frac{4}{3}\)(93 – r23) = 36 × 8 ⇒ 92 – r23 = \(\frac{{108\, \times \,8}}{4}\)
⇒ r23 = 93 – 108 × 2 = 729 – 216 ⇒ r23 = 513
⇒ r2 = (Internal radius of the shell) = \(\sqrt[3]{{513}}\) ≅ 8cm
⇒ Internal diameter of the shall
= 8 cm × 2 ≅ 16 cm
Example 16: The radius of the internal and external surface of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cylinder of height 10\(\frac{2}{3}\) cm. Find the diameter of the base of the cylinder.
Solution: Here, radius of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively.
So, its volume = \(\left[ {\frac{4}{3}\pi \,({5^3}\,–\,{3^3})} \right]\) cm3
= \(\left[ {\frac{4}{3}\pi \, \times (125\,–\,27)} \right]\) cm3 = \(\left( {\frac{4}{3}\,\pi \, \times \,98} \right)\) cm3
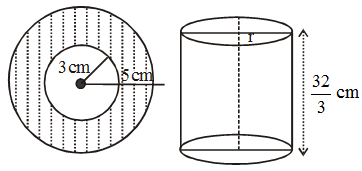
Let r be the radius of the right circular cylinder of height \(\frac{32}{3}\) cm.
Its volume = πr2h = \(\left( {\pi \, \times \,{r^2}\, \times \frac{{32}}{3}} \right)\)cm3
We have
Volume of the spherical shell = volume of the right circular cylinder
⇒ \(\frac{4}{3}\)π × 98 = π × r2 × \(\frac{32}{3}\)
⇒ 392 = 32r2 ⇒ r2 = \(\frac{392}{32}\) = \(\frac{49}{4}\)
⇒ r = \(\sqrt {\frac{{49}}{2}} \,\, = \,\,\frac{7}{2}\) = 3.5 cm
Hence, diameter of the right circular cylinder
= 2r = 2 × 3.5 cm = 7 cm
Example 17: A spherical ball of lead 3cm in diameter is melted and recast into three spherical balls. The diameters of two of these are 1 cm and 1.5cm. Find the diameter of the third ball.
Solution: It is given that
The diameter of a spherical ball = 3cm
⇒ radius of it = 1.5 cm = \(\frac{3}{2}\) cm
So, volume of it = \(\left[ {\frac{4}{3}\pi \, \times \,{{\left( {\frac{3}{2}} \right)}^3}} \right]\) cm3
= \(\left( {\frac{4}{3}\pi \, \times \,\frac{3}{2}\, \times \,\frac{3}{2}\, \times \,\frac{3}{2}} \right)\) cm3 = \(\frac{{108\pi }}{{24}}\) cm3 = \(\frac{{9\pi }}{2}\) cm2
This spherical ball is melted and recast into three small spherical balls. The diameters of two of these are 1 cm and 1.5 cm respectively.
So, volume of the two spherical balls.
= \(\left[ {\frac{4}{3}\pi \,\, \times \,\left\{ {{{\left( {\frac{1}{2}} \right)}^3}\, + \,{{\left( {\frac{3}{4}} \right)}^3}} \right\}} \right]\) cm3
= \(\left[ {\frac{4}{3}\pi \,\left( {\frac{1}{8}\, + \,\frac{{27}}{{64}}} \right)} \right]\)
cm3
= \(\left( {\frac{4}{3}\,\pi \, \times \,\frac{{35}}{{64}}} \right)\) cm3 = \(\frac{{140\,\pi }}{{192}}\) cm3
Let r be the radius of the third small spherical ball.
Thus, volume of the third ball = volume of the big spherical ball – sum of volume of two small spherical balls.
⇒ \(\frac{4}{3}\)πr3 = \(\frac{{9\pi }}{2} – \frac{{140\pi }}{{192}}\)⇒ \(\frac{4}{3}\) r3 = \(\frac{{9}}{2} – \frac{{140}}{{192}}\) = \(\frac{{864\,–\,140}}{{192}}\) = \(\frac{{724}}{{192}}\)
⇒ r3 = \(\frac{{724\, \times \,3}}{{4 \times 192}}\) = \(\frac{{181}}{{64}}\) ⇒ r = \(\sqrt[3]{{\frac{{181}}{{64}}}}\) cm
Hence, diameter of the 3rd spherical ball = 2r
= 2 × \(\frac{{\sqrt[3]{{181}}}}{{\sqrt[3]{{64}}}}\) = 2 × \(\frac{{\sqrt[3]{{181}}}}{4}\) = \(\frac{{\sqrt[3]{{181}}}}{2}\) cm
Example 18: A cylindrical container is filled with ice-cream whose diameter and the height are 12cm and 15cm respectively. The whole ice-cream is distributed to 10 children in equal inverted cones having hemispherical tops. Find the diameter of the ice-cream, if the height of the conical part is twice the diameter of its base.
Solution: We have radius of the cylindrical container = r = \(\frac{12}{2}\) = 6cm and height of it (h) = 15cm.
So, its volume = πr2h = (π × 62 × 15) cm3
= (π × 36 × 15) cm3 = 540 πcm3
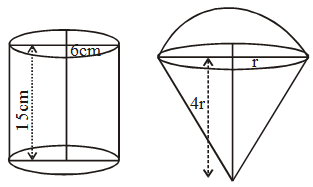
Let radius of the hemispherical part of the ice-cream = radius of the base of the conical part of the ice-cream = r
So, height of the conical part of the icecream = 4r
So, the volume of one ice-cream = volume of the hemispherical part + volume of the conical part.
= \(\left( {\frac{2}{3}\,\pi {r^3}\, + \,\frac{1}{3}\,\pi {r^2}\, \times \,4r} \right)\) cm3
= \(\left( {\frac{2}{3}\,\pi {r^3}\, + \,\frac{4}{3}\,\pi {r^3}} \right)\) cm3 = (2πr3) cm3
Volume of 10 ice-cream
= (10 × 2πr3)cm3 = (20πr3) cm3
Here, volume of 10 ice-cream = volume of the cylindrical container
⇒ 20πr3 = 540π ⇒ 20r3 = 540
⇒ r3 = \(\frac{{540}}{{20}}\) = 27 ⇒ r = \(\sqrt[3]{{27}}\) = 3 cm
Hence, the required diameter of the ice-cream
= 2r = 2 × 3 = 6cm
Example 19: Water flows out through a circular pipe, whose internal diameter is 2cm, at the rate of 0.7m/sec into a cylindrical tank, the radius of whose base is 40cm. By how much will the level of water rise in half an hour ?
Solution: We have volume of water flows out through a circular pipe in 1 second = volume of a cylinder of the base of radius 1 cm (r = \(\frac{2}{2}\) = 1 cm) and height 70 cm (h = 0.7m = 70 cm)
= πr2h = \(\left( {\frac{{22}}{7}\, \times \,{1^2}\, \times \,70} \right)\) cm3 = 220 cm3
So, volume of water passed through the pipe into the cylindrical tank in 1800 seconds \(\left( {\frac{1}{2}\,hour = \,\frac{{3600}}{2}\, = \,1800\sec } \right)\) = (220 × 1800) cm3 =396000 cm3
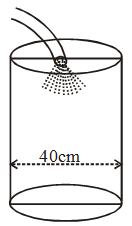
Thus, rise in the level of water in 1800 sec or half an hour
= \(\frac{{Total\,\,volume\,\,of\,\,water\,\,poured\,\,{\mathop{\rm int}} o\,\,the\,\,cylindrical\,\,\tan k}}{{Area\,\,of\,\,base\,\,of\,\,the\,\,cylindrical\,\,\tan k}}\)
= \(\frac{{396000\,\,c{m^3}}}{{\pi \, \times \,{{40}^2}c{m^2}}}\) (radius of the base of the cylindrical tank = 40 cm)
= \(\left( {\frac{{396000\,\,c{m^3}}}{{\frac{{22\, \times \,1600}}{7}\,c{m^2}}}} \right)\) = \(\left( {\frac{{396000\, \times \,\,7}}{{22\, \times \,\,1600}}} \right)\) cm
= 78.75 cm ≅ 79 cm
Hence, water rise upto 79 cm in half an hour
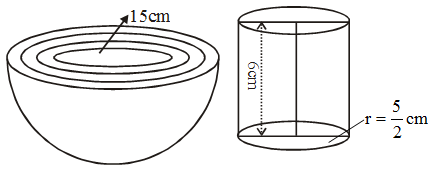
Example 20: A hemispherical bowl of internal radius 15cm is full of a liquid. The liquid is to be filled into some bottles of cylindrical in shape whose diameters and heights are 5 cm and 6 cm respectively. Find the number of bottles necessary to empty the bowl.
Solution: We have internal radius of the hemispherical bowl = R = 15 cm.
So, its volume = \(\frac{2}{3}\)π × R3
= \(\left[ {\frac{2}{3}\, \times \,\pi \, \times {{(15)}^3}} \right]\) cm3 = \(\left( {\frac{2}{3}\, \times \,\pi \, \times \,15\, \times \,15\, \times \,15} \right)\) cm3
= 10 × 15 × 15 πcm3 = 2250 πcm3
So, volume of the entire liquid = 2250 pcm3
The liquid is to be filled into some bottles of cylindrical in shape whose diameters and heights are 5 cm and 6 cm respectively. So, radius of the cylindrical bottle = \(\frac{5}{2}\)cm and height of it = 6cm
So, volume of one cylindrical bottle = πr2h
= \(\left( {\pi \, \times \,\frac{5}{2}\, \times \,\frac{5}{2}\, \times \,\,6} \right)\) cm3 = \(\left( {\frac{{75\pi }}{2}} \right)\) cm3
So, the number of bottles necessary to empty the hemispherical bowl
= \(\frac{{Volume\,\,of\,\,the\,\,entire\,\,liquid\,\,in\,\,the\,\,bowl}}{{Volume\,of\,\,one\,\,cylindrical\,\,bottle}}\)
= \(\frac{{2250c{m^3}}}{{\frac{{75\pi }}{2}\,\,c{m^3}}}\) = \(\frac{{2250\, \times 2}}{{75}}\) = 60
Example 21: A hemispherical tank of radius \(1\frac{3}{4}\)m is full of water. It is connected with a pipe which empties it at the rate of 7 lt/sec. How much time will it take to empty the tank completely ?
Solution: We have radius of the hemispherical tank
= \(1\frac{3}{4}\) = \(\frac{7}{4}\) m. It is full of water.
So, volume of entire water in the hemispherical tank
= \(\left[ {\frac{4}{3}\pi \, \times \,{{\left( {\frac{7}{4}} \right)}^3}} \right]\) m3= \(\left( {\frac{4}{3}\, \times \,\frac{{22}}{7}\, \times \,\frac{7}{4}\, \times \,\frac{7}{4}\, \times \,\frac{7}{4}} \right)\) m3
This tank is connected with a pipe which empties it at the rate of 7lt/sec.
So, volume of water flows out in 1 sec = 7 litre
= (7 × 1000)cm3 = 7000 cm3
= \(\left( {\frac{{7000}}{{100\, \times \,100\, \times \,100}}} \right)\) m3
Thus, total time will be taken to empty the tank full of water
= \(\left( {\frac{4}{3}\, \times \,\frac{{22}}{7}\, \times \,\frac{7}{4}\, \times \,\frac{7}{4}\, \times \,\frac{7}{4}} \right)\) ÷ \(\left( {\frac{{7000}}{{100\, \times \,100\, \times \,100}}} \right)\)
= \(\left( {\frac{{22\,\, \times \,49}}{{48}}\,\, \div \,\frac{7}{{1000}}} \right)\) sec
= \(\frac{{22\, \times \,49\,\, \times \,\,1000}}{{48\, \times 7}}\) sec = \(\frac{{19250}}{{12}}\) sec
= \(\left( {\frac{{19250}}{{12\, \times \,60}}} \right)\) min = \(\frac{{1925}}{{72}}\)
min = 26.73 minutes
Hence, the required time is 26.73 minutes.
Example 22: A hemispherical bowl of internal radius 9cm is full of liquid. This liquid is to be filled into cylindrical shaped small bottles each of diameter 3 cm and height 4 cm. How many bottles are necessary to empty the bowl ?
Solution: Volume of the hemispherical bowl
= \(\frac{2}{3}\)πR3 = \(\frac{2}{3}\) × \(\frac{22}{7}\) × (9)3
(R = Internal radius of the hemispherical bowl = 9 cm)
= \(\left( {\frac{2}{3}\, \times \,\frac{{22}}{7}\, \times \,9\,\, \times \,9\,\, \times \,9} \right)\) cm3
So, volume of the liquid in the bowl
= \(\left( {\frac{2}{3}\, \times \,\frac{{22}}{7}\, \times \,9\,\, \times \,9\,\, \times \,9} \right)\) cm3
Volume of a bottle = πr2h = \(\frac{22}{7}\) × \({\left( {\frac{3}{2}} \right)^2}\) × 4
(r = radius of the cylindrical bottle = \(\frac{3}{2}\) cm and height (h) = 4 cm)
= \(\frac{{22}}{7} \times \frac{9}{4} \times 4 = \frac{{198}}{7}\) cm3.
Number of bottles required to empty the bowl
= \(\frac{{Volume\,\,of\,\,the\,\,liquid\,\,in\,\,the\,\,bowl}}{{volume\,\,of\,\,the\,\,one\,\,bottle}}\)
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 9 × 9 × 9 ÷ \(\frac{{198}}{7}\)
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 9 × 9 × 9 × \(\frac{{7}}{198}\) = 54
Hence, the required number of bottle necessary to empty the bowl is 54.
Example 23: Water in a canal, 30 dm wide and 12 dm deep is flowing with velocity of 10 km per hour. How much area will it irrigate in 30 minutes, if 8cm of standing water is required for irrigation ?
Solution: We have
30 dm = \(\frac{30}{10}\) m, 12dm = \(\frac{12}{10}\) m
10 km = 10 × 1000 m
Volume of water flowing in canal in 1 hour
= \(\frac{30}{10}\) × \(\frac{12}{10}\) × 10 × 1000 = 36000 m3.
Volume of water flowing in canal in 30 minutes
= \(\left( {\frac{1}{2}\,hour} \right) = \frac{{36000}}{2}\) = 18000 m3.
Then Area that will be irrigated in \(\frac{1}{2}\) hour
= \(\frac{{volume}}{{height}}\) = \(\frac{{18000{m^3}}}{{8m}}\)
= \(\left( {\frac{{18000\, \times \,100}}{8}} \right)\) m2 = 225000 m2
Hence, the required amount of standing water needed is 225000 m2.
Example 24: Water flows at the rate of 10m per minutes through a cylindrical pipe having its diameter as 5 mm. How much time will it take to fill a conical vessel whose diameter of base is 40 cm and depth 24 cm ?
Solution: We have diameter = 5mm
⇒ radius = \(\frac{5}{2}\)mm = \(\frac{5}{{10\, \times \,2}}\) cm
Also 10m = (10 × 100) cm
Volume of water that flows through the cylindrical pipe in 1 minute
= \(\left[ {\frac{{22}}{7}\, \times \,{{\left( {\frac{5}{{10\,\, \times \,\,2}}} \right)}^2}\, \times \,\,10\,\, \times \,\,100} \right]\) cm3
= \(\left[ {\frac{{22}}{7}\, \times \,\frac{{5\,\, \times \,5}}{{20\, \times \,20}} \times 1000} \right]\) cm3 = \(\frac{{1375}}{7}\) cm3
Volume of the conical vessel with radius 20 cm \(\left( {\frac{{40}}{2}\, = \,20cm} \right)\) cm3 and depth 24 cm
= \(\left[ {\frac{1}{3}\,\, \times \,\,\frac{{22}}{7}\, \times \,{{(20)}^2}\, \times \,\,24} \right]\) cm3
= \(\left( {\frac{1}{3}\, \times \,\frac{{22}}{7} \times 20 \times 20 \times 24} \right)\)
Time taken to fill the conical vessel
= \(\left( {\frac{1}{3}\, \times \,\frac{{22}}{7} \times 20 \times 20 \times 24} \right)\) ÷ \(\frac{{1375}}{7}\)
= \(\frac{1}{3}\, \times \,\frac{{22}}{7}\, \times \,\frac{{20\, \times 20\, \times \,\,24\, \times \,7}}{{1375}}\)
= \(\frac{{1478400}}{{28875}}\) = 51.2 minutes
Hence, the required time needed is 51.2 minutes.
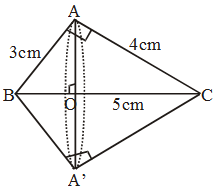
Example 25: A right triangle with sides 3 cm and 4 cm is revolved around its hypotenuse. find the volume of the double cone thus generated.
Solution: Hypotenuse BC of the right triangle BAC, right-angled at A = \(\sqrt {{3^2}\, + \,{4^2}} \,\, = \,\,\sqrt {9\, + \,16} \, = \,5cm\)
Since the triangle is revolved around the hypotenuse, therefore AO is the radius of the common base of the double cone so formed.
Height of the cone BAA‘ is BO and its slant height is 3cm. Height of the cone CAA‘ is CO and its slant height is 4cm
In the right triangles AOB and BAC, we have
So, ∠B = ∠B (common)
∠ BOA = ∠BAC = 90º
Thus, by AA – criterion of similarity, we have
∆AOB ~ ∆BAC
\(\frac{{AO}}{{AC}} = \frac{{AB}}{{BC}}\)
⇒ \(\frac{{AO}}{4}\, = \,\frac{3}{5}\) ⇒ AO = \(\frac{3}{5}\) × 4 = \(\frac{12}{5}\) cm
and \(\frac{{BO}}{{AB}} = \frac{{AB}}{{BC}}\)
⇒ \(\frac{{BO}}{3} = \frac{3}{5}\) ⇒ BO = \(\frac{{3\, \times \,3}}{5}\) = \(\frac{9}{5}\) cm
Now, CO = BC – BO = 5 – \(\frac{9}{5}\) = \(\frac{16}{5}\) cm.
Volume of cone BAA‘
= \(\frac{1}{3}\)πr2h = \(\frac{1}{3}\)× \(\frac{{22}}{7}\) × (AO)2 × BO
= \(\frac{1}{3}\) × \(\frac{{22}}{7}\, \times \,\frac{{12}}{5}\, \times \,\frac{{12}}{5}\, \times \,\frac{9}{5}\) = \(\frac{{9504}}{{875}}\) cm3
Volume of conc CAA‘ = \(\frac{1}{3}\)πr2h
= \(\frac{1}{3}\) × \(\frac{{22}}{7}\) × (AO)2 × CO
= \(\frac{1}{3}\) × \(\frac{{22}}{7}\) × \(\frac{{12}}{5}\) × \(\frac{{12}}{5}\) × \(\frac{{16}}{5}\)
= \(\frac{{16896}}{{875}}\) cm3
So, volume of the double cone thus formed
= \(\frac{{9504}}{{875}} + \frac{{16896}}{{875}} = \frac{{26400}}{{875}}\)
= \(\frac{{1056}}{{35}}\) = 30\(\frac{6}{{35}}\) cm3
Hence, the required volume is 30\(\frac{6}{{35}}\) cm3.