Representing Irrational Numbers On The Number Line


Represent √2 & √3 on the number line:
Greeks discovered this method. Consider a unit square OABC, with each side 1 unit in lenght. Then by using pythagoras theorem
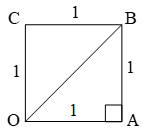
\(OB=\sqrt{1+1}=\sqrt{2}\)
Now, transfer this square onto the number line making sure that the vertex O coincides with zero
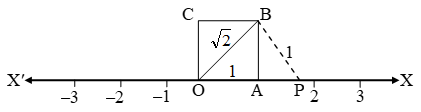
With O as centre & OB as radius, draw an arc, meeting OX at P. Then
OB = OP = √2 units
Then, the point represents √2 on the number line
Now draw, BD ⊥ OB such that BD = 1 unit join OD. Then
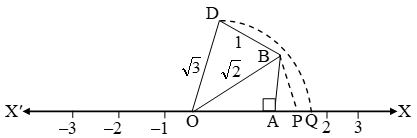
OD = \(\sqrt{{{(\sqrt{2})}^{2}}+{{(1)}^{2}}}=\sqrt{3}\) = units With O as centre & OC as radius, draw an arc, meeting OX at Q. Then
OQ = OD = √3 units
Then, the point Q represents √3 on the real line
Remark: In the same way, we can locate √n for any positive integer n, after \(\sqrt{n-1}\) has been located.
Existence of √n for a positive real number:
The value of √4.3 geometrically : –
Draw a line segment AB = 4.3 units and extend it to C such that BC = 1 unit.
Find the midpoint O of AC.
With O as centre and OA a radius, draw a semicircle.
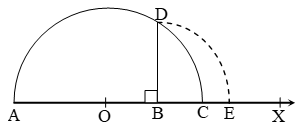
Now, draw BD ⊥ AC, intersecting the semicircle at D. Then, BD = √4.3 units.
With B as centre and BD as radius, draw an arc, meeting AC produced at E.
Then, BE = BD = √4.3 units