What is the Radius of a Right Circular Cylinder
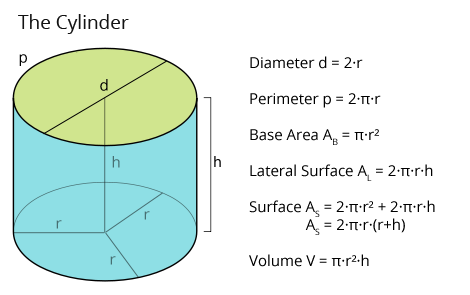
If r and h denote respectively the radius of the base and height of a right circular cylinder, then –
- Area of each end = πr2
- Curved surface area = 2πrh = (circumference) height
- Total surface area = 2πr (h + r) sq. units.
- Volume = πr2h = Area of the base × height
where, π = \(\frac{{22}}{{7}}\) or 3.14
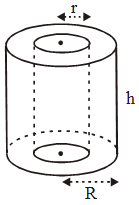
If R and r (R > r) denote respectively the external and internal radii of a hollow right circular cylinder, then –
Let external radius = R, Internal radius = r, height = h. Then,
- Outer curved surface area = 2πRh
- Inner curved surface area = 2πrh
- Area of each end = π (R2 – r2)
- Curved surface area of hollow cylinder = 2π (R + r) h
- Total surface area = 2π (R + r) (R + h – r)
- Volume of material = πh (R2 – r2)
Read more about Area of a Right Circular Cone
Right Circular Cylinder Example Problems with Solutions
Example 1: The inner diameter of a circular well in 2 m and its depth is 10.5 m. Find :
(i) the inner curved surface area of the well.
(ii) the cost of plastering this curved surface area at the rate of Rs. 35 per m2.
Solution: Given : Radius = \(\frac{1}{2} \times 2\,m\) = 1m i.e., r = 1 m and depth = 10.5 m i.e., h = 10.5 m
(i) The inner curved surface area of the well = 2πrh = 2 × \(\frac{{22}}{7} \times 1 \times 10.5\) m2 = 66 m2
(ii) The cost of plastering
= Area to be plastered × Rate
= 66 × Rs. 35 = Rs. 2,310
Example 2: In a hot water heating system there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
Solution: Given : Length of the cylindrical pipe = 28 m i.e., h = 2800 cm and, its radius = \(\frac{1}{2}\) × diameter = \(\frac{1}{2}\) × 5 cm = 2.5 cm.
∴ The total radiating surface in the system
= curved surface area of the pipe
= 2πrh = 2 × \(\frac{22}{7}\) × 2.5 × 2800 cm2
= 44000 cm2
It is not clear from the question that how the cylindrical pipe is used. We can take the radiating surface of the system
= Total surface area of the pipe
= 2πr (r + h) = 2 × \(\frac{{22}}{7} \times 2.5\) (2.5 + 2800) cm2
= 44039.29 cm2
Example 3: Find :(i) the lateral or curved surface area of a cylindrical patrol storage tank that is 4.2 m in diameter and 4.5 m high.
(ii) how much steel was actually used if \(\frac{1}{12}\) of the steel actually used was wasted in making the closed tank.
Solution: (i) Given : r = \(\frac{{4.2}}{2}m\) = 2.1 m and h = 4.5 m
∴ Curved surface area of the tank
= 2πrh = 2 × \(\frac{{22}}{7} \times 2.1\) × 4.5 m2 = 59.4 m2
(ii) Let the steel actually used be x m2
∴ x –\(\frac{1}{{12}}x\) = 59.4 ⇒ \(\frac{11}{{12}}x\) = 59.4
⇒ x = 59.4 × \(\frac{12}{{11}}\) = 64.8 m2
∴ Actual amount of steel used = 64.8 m2
Example 4: The figure, given alongside, shows the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame . Find how much cloth is required for covering the lampshade.
 Solution: Given : The height of the lampshade = 30 cm.
Solution: Given : The height of the lampshade = 30 cm.
∵ A margin of 2.5 cm is required for folding its over and bottom of the frame ; the resulting height of the cloth required in the shape of the cylinder = (30 + 2.5 + 2.5) cm = 35 cm.
∴ For the cloth, which must be in the
shape of a cylinder with height 35 cm and
radius \(\frac{{20}}{2}cm\) = 10 cm.
i.e., h = 35 cm and r = 10 cm.
∴ Area of the cloth required for covering the lampshade.
= 2πrh = 2 × \(\frac{22}{7}\) × 10 × 35 cm2
= 2200 cm2 .
Example 5: The total surface area and the curved surface area of a cylinder are in the ratio 5 : 3. Find the ratio between its height and its diameter.-
Solution: Required = \(\frac{{Height}}{{Diameter}} = \frac{h}{d} = \frac{h}{{2r}}\)
According to the given statement :
\(\frac{{2\pi r(h + r)}}{{2\pi rh}} = \frac{5}{3}\) ⇒ \(\frac{{h + r}}{h} = \frac{5}{3}\)
⇒ 5h = 3h + 3r
i.e., 2h = 3r
⇒ \(\frac{h}{r} = \frac{3}{2}\)
and \(\frac{h}{{2r}} = \frac{3}{{2 \times 2}} = \frac{3}{4}\) = 3 : 4
Example 6: A soft drink is available in two packs of different shapes : (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
Solution: (i) Volume of soft drink in the tin can
= Volume of the tin can
= Its length × breadth × height
= 5 cm × 4 cm × 15 cm = 300 cm3
(ii) Volume of soft drink in the plastic cylinder
= πr2h = \(\frac{{22}}{7} \times \frac{7}{2} \times \frac{7}{2} \times 10\,\,cm\)
[ ∵ r = \(\frac{{diameter}}{2} = \frac{7}{2}\,\,cm\) ]
= 385 cm3
Clearly, plastic container has greater capacity by
385 cm3 – 300 cm3 = 85 cm3
Example 7: The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many liters of water can it hold? (1000 cm3 = 1 ℓ)
Solution: Let the radius of the base of the cylindrical vessel be r cm.
∴ 2πr = 132 [∵ circumference = 2πr]
⇒ 2× \(\frac{{22}}{7} \times r = 132\)
⇒ r = \(\frac{{132 \times 7}}{{2 \times 22}}cm = 21\,\,cm\)
Now, radius (r) = 21 cm and height (h) = 25 cm
⇒ Volume of the cylindrical vessel = πr2h
= \(\frac{22}{7}\) × 21 × 21× 25 cm2 = 34560 cm3
∴ Vol. of water which this vessel can hold
= Volume of the vessel = 34560 cm3
= \(\frac{{34560}}{{1000}}\ell\) [∵ 1000 cm3 = 1 ℓ]
= 34.650 ℓ
Example 8: A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution: Radius of cylindrical bowl \(\frac{7}{2}cm\) = i.e., r = \(\frac{7}{2}cm\) and the height of the soup in a bowl h = 4 cm
∴ Volume of soup required for 1 patient
= πr2h = \(\frac{{22}}{7} \times \frac{7}{2} \times \frac{7}{2} \times 4\,c{m^3}\)
= 154 cm3.
⇒ Volume of soup required for 250 patients.
= 250 × 154 cm3 = 38500 cm3
Example 9: If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find:
(i) radius of its base
(ii) its volume. (Use π = 3.14)
Solution: Given. 2πrh = 94.2 cm2 and h = 5 cm
(i) 2πrh = 94.2 cm2
⇒ 2 × 3.14 × r × 5 = 94.2
⇒ r = \(\frac{{94.2}}{{2 \times 3.14 \times 5}}cm\) = 3 cm .
(ii) Its volume = πr2h
= 3.14 × 3 × 3 × 5 cm2
= 141.3 cm3
Example 10: A hollow cylinder is 35 cm in length (height). Its internal and external diameters are 8 cm and 8.8 cm respectively. Find its :
(i) outer curved surface area
(ii) inner curved surface area
(iii) area of cross-section
(iv) total surface area.
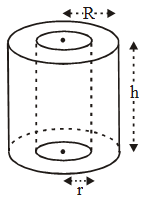 Solution: The height of the cylinder h = 35 cm
Solution: The height of the cylinder h = 35 cm
The internal radius r = \(\frac{8}{2}cm\) = 4 cm
The external radius R = \(\frac{8.8}{2}cm\) = 4.4 cm
(i) Outer curved surface area = 2πRh
= 2 × \(\frac{{22}}{7} \times 4.4 \times 35c{m^2}\) = 968 cm2
(ii) Inner curved surface area = 2πrh
= 2 × \(\frac{{22}}{7} \times 4 \times 35c{m^2}\) = 880 cm2
(iii) The cross-section of a hollow cylinder is like a ring with external radius R = 4.4 cm and internal radius r = 4 cm.
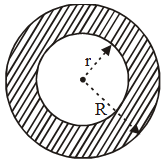 ∴ Area of cross-section = πR2 – πr2
∴ Area of cross-section = πR2 – πr2
= π (R2 – r2) = \(\frac{{22}}{7}({4.4^2}–{4^2})\,c{m^2}\)
= \(\frac{{22}}{7}(4.4 + 4)\,(4.4 – 4)\,c{m^2}\)
= \(\frac{{22}}{7} \times 8.4 \times 0.4\,c{m^2}\)
= 10.56 cm2
Example 11: Find the total surface area of a hollow cylindrical pipe of length 50 cm, external diameter 12 cm and internal diameter 9 cm.
 Solution: Given : Height (h) = 50 cm, external radius (R) = 6 cm and internal radius (r) = 4.5 cm
Solution: Given : Height (h) = 50 cm, external radius (R) = 6 cm and internal radius (r) = 4.5 cm
∵ Total surface area of the hollow cylinder
= External C.S.A + Internal C.S.A + 2 × Area of cross-section
= 2πRh + 2πrh + 2π (R2 – r2)
= 2π (R + r)h + 2π (R + r) (R – r)
= 2 × \(\frac{22}{7}\) × (6 + 4.5) × 50 + 2 × \(\frac{22}{7}\) × (6 + 4.5) (6 – 4.5) cm2
= \(\frac{{44}}{7} \times 10.5\) × 50 + \(\frac{{44}}{7} \times 10.5 \times 1.5c{m^2}\)
= 3300 cm2 + 99 cm2 = 3399 cm2
Example 12: The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
Solution: Since, inner diameter = 24 cm
⇒ inner radius (r) = \(\frac{{24}}{2}cm\) = 12 cm
Since, outer diameter = 28 cm
⇒ outer radius (R) = \(\frac{{28}}{2}cm\) = 14 cm
Also, given that height (h) = 35 cm
∴ Volume of wood in the pipe = π (R2 – r2)h
= \(\frac{{22}}{7}\) (142 –122) × 35 cm3 = 5720 cm3
Since, mass of 1 cm3 of wood = 0.6 gm
⇒ Mass of 5720 cm3 of wood = 0.6 × 5720 gm = 3432 gm
∴ Mass of the pipe = mass of wood
= 3432 gm
= 3.432 kg
Example 13: A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
Solution: Clearly, for wooden part, which is the form of a hollow cylinder :
External radius (R) = \(\frac{7}{2}mm\) = 3.5 mm
= 0.35 cm
Internal radius (r) = \(\frac{1}{2}mm\) = 0.5 mm
= 0.05 cm
And, height (length) = 14 cm.
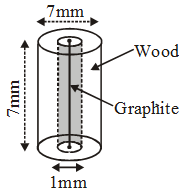 ∴ Volume of the wood = π (R2 – r2)h
∴ Volume of the wood = π (R2 – r2)h
= \(\frac{{22}}{7}\) × [(0.35)2 – (0.05)2] × 14 cm3
= \(\frac{{22}}{7}\) × 0.12 × 14 cm3 = 5.28 cm3
And, volume of graphite = π r2h
= \(\frac{{22}}{7}\) × (0.05)2 × 14 cm3 = 0.11 cm3
Example 14: The internal radius of a hollow cylinder is 8 cm and thickness of its wall is 2 cm. Find the volume of material in the cylinder, if its length is 42 cm.
Solution: Since, internal radius = 8 cm π r = 8 cm,
thickness of the wall of the cylinder = 2 cm.
∴ Its external radius = 8 cm + 2 cm = 10 cm i.e., R = 10 cm.
Also, length (height) of the cylinder = 42 cm i.e., h = 42 cm.
∴ Volume of material in the hollow cylinder.
= π (R2 –r2)h
= \(\frac{{22}}{7}\) [(10)2 – (8)2] × 42 cm3
= \(\frac{{22}}{7}\) × 36 × 42 cm3 = 4752 cm3
Example 15: The radii of two right circular cylinders are in the ratio 3 : 4 and their heights are in the ratio 6 : 5. Find the ratio between their curved (lateral) surface areas.
Solution: If the radii of two cylinders be r1 and r2,
let r1 = 3x and r2 = 4x.
Similarly, if the heights of two cylinders be h1 and h2, let h1 = 6y and h2 = 5y.
Ratio between their C.S.A.
= \(\frac{{2\pi {r_1}{h_1}}}{{2\pi {r_2}{h_2}}}\) = \(\frac{{2\pi \times 3x \times 6y}}{{2\pi \times 4x \times 5y}} = \frac{9}{{10}}\)
= 9 : 10