Kerala Plus One Maths Chapter Wise Previous Questions Chapter 2 Relations and Functions
Plus One Maths Relations and Functions 3 Marks Important Questions
Question 1.
Let A = {1,2,3,4} and B = {1,4,5} be two sets. (IMP-2011)
If R is the relation”<” from A to B then )
i) Write R in Roster form.
ii) Write Domain and Range of R.
iii) Find the number of relations from AtoB.
Answer:
i) R = {(1,4), (1,5), (2,4), (2,5), (3,4), (3,5), (4,5)}
ii) Domain of R = {1,2,3,4}; Range of R = {4,5}
iii) Number of relations from A to B = 24 x 3 =212
Question 2.
\(\left(\frac{2 x}{5}+1, y-\frac{3}{4}\right)=\left(\frac{1}{5}, \frac{1}{4}\right)\) find xand y (IMP-2012)
Answer:
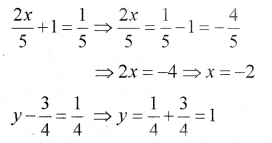
Question 3.
Let A = {1,2,3}; B = {3,4}. Write a relation from A and B having 5 elements. Write its domain, co-domain and range. (IMP-2012)
Answer:
R = {(1,3), (1,4), (2,3), (3,4), (3,3)}
Domain of R = {1,2,3}
Range of R = {3,4}
Co-domain of R = {3,4} = B
Question 4.
The function f is defined by (IMP-2012)
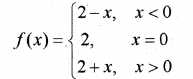
Draw the graph of Find f(x)
Answer:
For x < 0
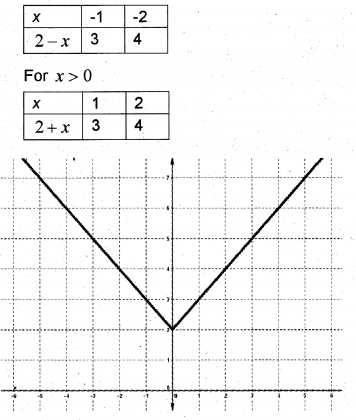
Question 5.
5. Let A = {1,2,3}, B={4,5} (MARCH- 2013)
i) Find A x B and B x A
ii) Find the number of relations from A to B.
Answer:
i) A x B = {(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)} B x A = {(4,1), (4,2), (4,3), (5,1), (5,2), (5,3)}
ii) n(R) = 22 x 3 = 26 = 64
Question 6.
i) Let A = {7,8} and B = {2,4,5}. Find A x B (MARCH – 2013)
ii) Determine the domain and range of the relation R defined by R={(x,y):y=x+1},
x ∈ {0,1,2,3,4,5,6}
Answer:
i) A x B = {(7,5), (7,4), (7,2), (8,5), (8,4), (8,2)}
ii) R= {(0,1),(1,2),(2,3),(3,4),(4,5),(5,6)}
Domain = {0,1,2,3,4,5}
Range = {1,2,3,4,5,6}
Question 7.
i) If A = {2,4}, B = {1,3,5}. Then the number of relations from A to B is …………. (IMP-2013)
ii) If P={-1,1}, form the set P x P x P
Answer:
i) number of relations from A to B 22 x 3 = 26 = 64
ii) P x P = {-1,1} x {-1,1} – {(-1,-1),(-1,1), (1-1), (1,1)}
P x P x P={(-1,-1), (-1,1), (1,-1),(1,1)} x {-1,1}
= {(-1,-1,-1),(-1-1,1),(-1,1,-1),(-1,1,1), (1,-1,-1), (1,-1,1), (1,1-1), (1,1,1)}
Question 8.
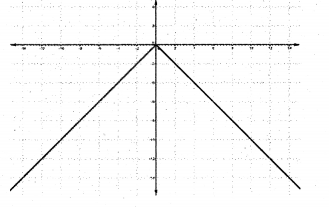
Consider the function f :R -> R defined by f(x) = -|x| (IMP-2013)
i) Find the domain and range of f.
ii) Draw the graph of f.
Answer:
i) Domain = R; Range = (-∝,0]
ii)
Plus One Maths Relations and Functions 4 Marks Important Questions
Question 1.
Consider the functions (MARCH- 2010)
\(f(x)=\sqrt{x-2}, \quad g(x)=\frac{x+1}{x^{2}-2 x+1}\)
Find
i) Domain of ‘f.
ii) Domain of ‘g’.
iii) (f + g)(x)
iv) (fg)(x)
Answer:

Question 2.
The Cartesian product P*P has 9 elements among which are found (- a, 0) and (a, 0). A relation from P to P is defined as (IMP- 2010)
R = {(x,y):x + y = 0)
i) Find P.
ii) Depict the relation using an arrow
diagram.
iii) Write down the domain and range of R,
iv) How many relations are possible from P to P?
Answer:
i) (-a,0), (a,0) are elements in P*P and P*P have 9 elements, implies P has 3 elements Therefore; P = {- a,a,0}
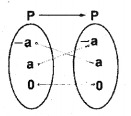
ii) Given; R = {(x,.y) : x + y
x = -a=>y = a=> (-a, a)
x = a =>y = -a => (a,-a)
x = 0=>y = 0 => (0,0)
iii) R = {{-a, a), (a-a), (0,0)}
Domain of R = {-a,a,0}; Range of R = {-a,a,0}
iv) Number of relation from P to P = 29
Question 3.
Consider the real function (MARCH-2012)
\(f(x)=\frac{x+2}{x-2}\)
i) Find the domain and range of thefunction.
ii) Prove that f(x)f(-x) + f(0) = 0
Answer:

Question 4.
i) Let P = {1,2}. Find P x P x P (MARCH-2014)
ii) Let A = {1,2,3,……..13,14},
R is the relation on A defined by R={(x,y):3x-y=0,x,y∈A}
a) Write R in a tabular form.
b) Find the domain and range of R.
Answer:
i) P x P x P = {(1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2)}
ii) R = {(1,3), (2,6), (3,9), (4,12)}
Domain = {1,2,3,4}
Range = {3,6,9,12}
Question 5.
i) Write the domain and range of the relation (IMP-2014)
R = {(2,5),(3,10),(4,17),(5,26)}
ii) If f{x) – x² -3x and g(x) = x + 2 find (f + g)(x), (f – g)(x) and (fg)(x)
Answer:
i) Domain = {2,3,4,5}; Range = {5,10,17,26}
ii) (f – g)(x) = f(x) – g(x)
= x² – 3x + x + 2
=x²—2x + 2
(f – g)(x) = f(x) – g(x)
= x² – 3x – x – 2 =x²-4x – 2
(fg)(x) = f(x) x g(x)
= (x² —3x) x (x + 2) = x³ – x² – 6x
Question 6.
i) If P = {m,n}, Q = {n,m} ; state whether the following is TRUE or FALSE (MAY-2016)
P x Q – {(m,n),(n,m)}
ii) Write the relation R= {(x, x³), x is a prime number less than 10}, in roster form.
iii) Let A = {1,2,3,4} B = {1,5,9,11,15,16} and
f = {(1,5),(2,9),(3,1),(4,5),(2,1)}. State with the reason whether f is a relation or a function.
Answer:
i) False
ii) R = {(2,2³)(3,3³),(5,5³),(7,7³)}
= {(2,8)(3,27), (5,125), (7,343)}
iii) F is not a function since the element 2 has two images.
Plus One Maths Relations and Functions 6 Marks Important Questions
Question 1.
Let R be the set of Reals. Define a function (IMP-2011)
f : R→R by f(x) = 2x²-1
i) Find \(\frac{f(-1)+f(1)}{2}\)
ii) Find f[f(x)]
iii) Draw the graph of f(x)
Answer:
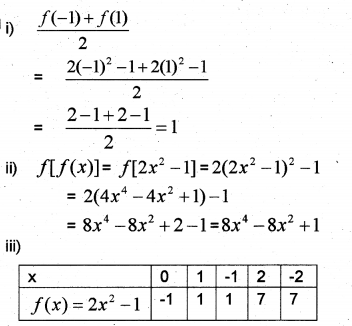
Question 2.
i) If A = {-1,1}, Find A x A. (MARCH-2014)
ii) Consider the relation R defined by R = {(x,x + l) : x ∈ {-1,1}} Write R in the roster form. Also find the range.
iii) Draw the graph of the function. y = x, x ∈ R
Answer:
i) A x A ={-1,1} x {-1,1}
= {(-1,-1), (-1,1), (1,-1), (1,1)}
ii) R = {(-1,0),(1,2)}; Range ={0,2}
iii)
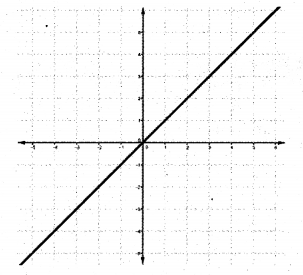
Question 3.
Let A = {1,2,3,4,5,6} be a set. Defined a relation R from A to A by R = {(x,y)/y = x+1} (IMP-2014)
i) Express R in the roster form.
ii) Represent the relation R using an arrow diagram.
iii) Write the domain and range of R.
Answer:
i) R = {(1,2),(2,3),(3,4),(4,5),(5,6)}
ii) Given; y = x +1
x = l =>j = 1 + 1 = 2; x = 2=> y = 3
x = 3 =>j = 4; x = 4 =>y = 5
x = 5=> y = 6
R = {(1,2), (2,3), (3,4), (4,5), (5,6)}
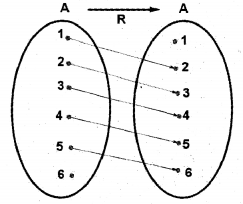
iii) Domain of R = {1,2,3,4,5}
Range of R = {2,3,4,5,6}
Codomain of R = {1,2,3,4,5,6}
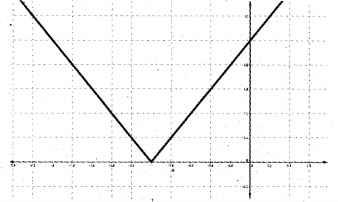
Question 4.
i) Find the domain of the function. (MARCH-2015)
\(f(x)=\frac{x^{2}+3 x+5}{x^{2}-5 x+4}\)
ii) Sketch the graph of the function
f(x) = |x + 1|
iii) Consider A = {1,2,3,5} and B = {4,6,9}. Define a relation
R : A → B by R = {(x,y): x – y is odd,x ∈ A,y ∈ B}.
Write R in roster form and find range of R.
Answer:
i) x² – 5x + 4 = 0 => (x-4)(x-l) = 0
Therefore f(x) is defined for all x∈R? , except x = 4 and x = 1. Hence the domain is R – {1,4}.
ii)
iii) R = {(1,4),(1,6),(2,9),(3,4),(3,6),(5,4),(5,6)}
Range = {4,6,9}
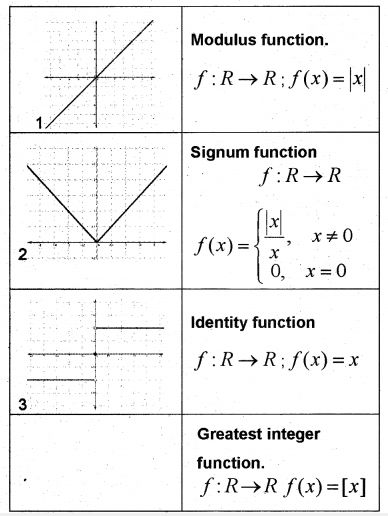
Question 5.
i) Match the following (IMP-2015)
ii) A = {1,2,3 ………. 14}. R is a relation from
A to A defined by R = {(x,y): 3x – y = 0,x,y ∈A}. Write the domain, range, co-domain of ,R.
Answer:
i) 1- Identity function, f :R →R : f(x) = x
2- Modulus function, f :R →R : f(x) = |x|
3 – Signum function f :R → R

Question 6.
i) If (x+1, y-2) = (3,1), write the values of x and y. (MARCH-2016)
ii) Let A = {1,2,3,4,5,} and B = {4,6,9} be two sets. Define a relation R from A to B by R = {(x,y): x – y} is a positive integer}
iii) Define the modulus function. What is its domain? Draw a rough sketch.
Answer:
i) Given; (x + l,y-2) = (3,1)
=> x + l = 3;
y – 2 = 1
=>x = 2; y = 3
ii) A x B= {(1,4),(1,6),(1,9),(2,4),(2,6),(2,9), (3,4),(3,6),(3,9),(4,4),(4,6)(4,9),(5,4),(5,6),(5,9)}
Then R = {(5,4)}
Question 7.
The domain of the function (MARCH-2017)
\(f(x)=\frac{1}{x-1}\)
(a) {1}
(b) R
(c) R – {1}
(d) R – {0}
ii) A relation R on set natural numbers is defined by R = {(x,y):y = x+5,x is a natural number less than 4, x, y ∈ N}
a) Write the relation in roster form.
b) Write the domain and range of the relation.
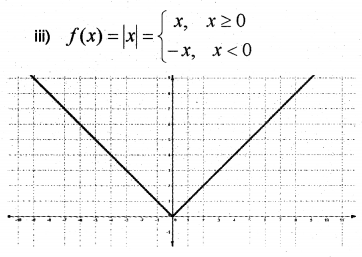
iii) Draw the graph of the relation
f(x) = |x|,x∈R
Answer:
i) c) R – {1}
ii) a) R = {(1,6), (2,7), (3,8)}
b) Domain = {1,2,3,}
Range of R = {6,7,8}
