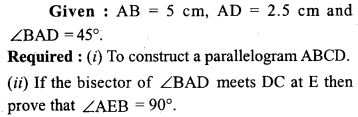Rectilinear Figures Class 9 ICSE ML Aggarwal

ML Aggarwal Class 9 Solutions Chapter 13 provides comprehensive guidance and step-by-step explanations for the concepts covered in this chapter Class 9 Mathematics. This chapter typically introduces fundamental mathematical concepts, laying the groundwork for future studies.

ML Aggarwal Class 9 Chapter 13 Solutions

ICSE Class 9 Maths Chapter 13 Solutions ML Aggarwal

Exercise 13.1

Question 1.
If two angles of a quadrilateral are 40° and 110° and the other two are in the ratio 3 : 4, find these angles.
Solution:

Question 2.
If the angles of a quadrilateral, taken in order, are in the ratio 1 : 2 : 3 : 4, prove that it is a trapezium.
Solution:

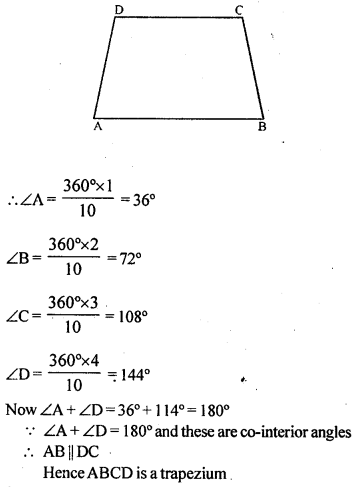
Question 3.
If an angle of a parallelogram is two-thirds of its adjacent angle, find the angles of the parallelogram.
Solution:

Question 4.
(a) In figure (1) given below, ABCD is a parallelogram in which ∠DAB = 70°, ∠DBC = 80°. Calculate angles CDB and ADB.
(b) In figure (2) given below, ABCD is a parallelogram. Find the angles of the AAOD.
(c) In figure (3) given below, ABCD is a rhombus. Find the value of x.

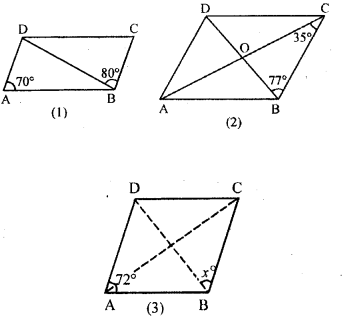
Solution:

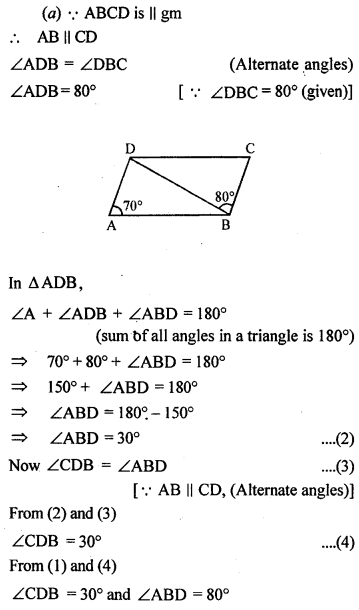
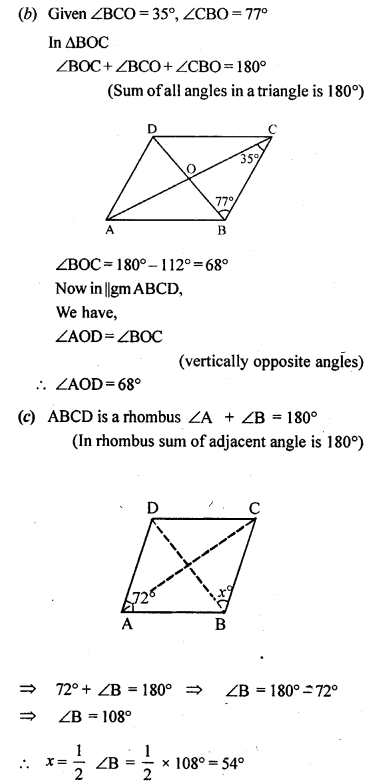
Question 5.
(a) In figure (1) given below, ABCD is a parallelogram with perimeter 40. Find the values of x and y.
(b) In figure (2) given below. ABCD is a parallelogram. Find the values of x and y.
(c) In figure (3) given below. ABCD is a rhombus. Find x and y.
Solution:

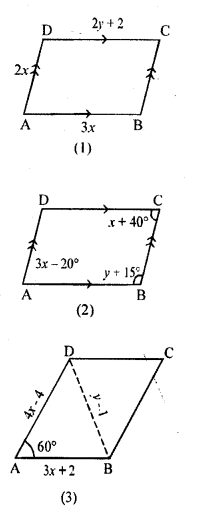
Question 6.
The diagonals AC and BD of a rectangle > ABCD intersect each other at P. If ∠ABD = 50°, find ∠DPC.
Solution:

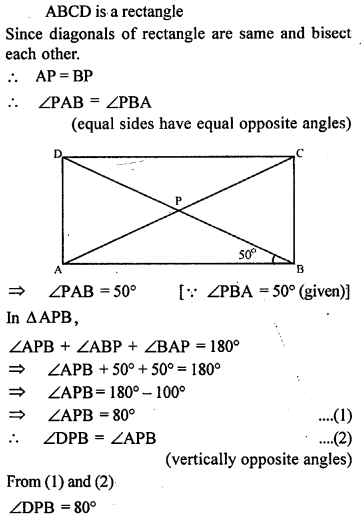
Question 7.
(a) In figure (1) given below, equilateral triangle EBC surmounts square ABCD. Find angle BED represented by x.
(b) In figure (2) given below, ABCD is a rectangle and diagonals intersect at O. AC is produced to E. If ∠ECD = 146°, find the angles of the ∆ AOB.
(c) In figure (3) given below, ABCD is rhombus and diagonals intersect at O. If ∠OAB : ∠OBA = 3:2, find the angles of the ∆ AOD.

Solution:

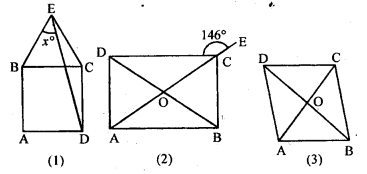
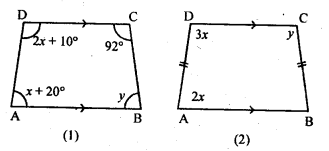
Question 8.
(a) In figure (1) given below, ABCD is a trapezium. Find the values of x and y.
(b) In figure (2) given below, ABCD is an isosceles trapezium. Find the values of x and.y.
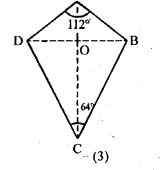
(c) In figure (3) given below, ABCD is a kite and diagonals intersect at O. If ∠DAB = 112° and ∠DCB = 64°, find ∠ODC and ∠OBA.


Solution:

Question 9.
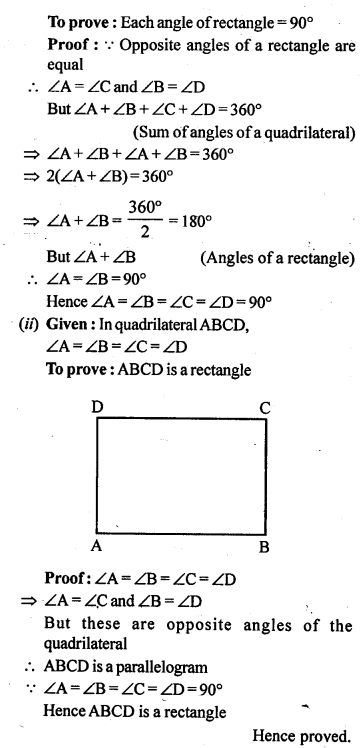
(i) Prove that each angle of a rectangle is 90°.
(ii) If the angle of a quadrilateral are equal, prove that it is a rectangle.
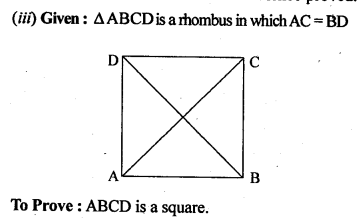
(iii) If the diagonals of a rhombus are equal, prove that it is a square.
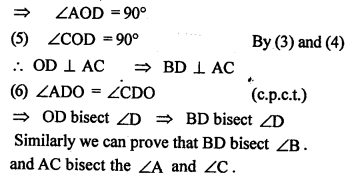
(iv) Prove that every diagonal of a rhombus bisects the angles at the vertices.
Solution:

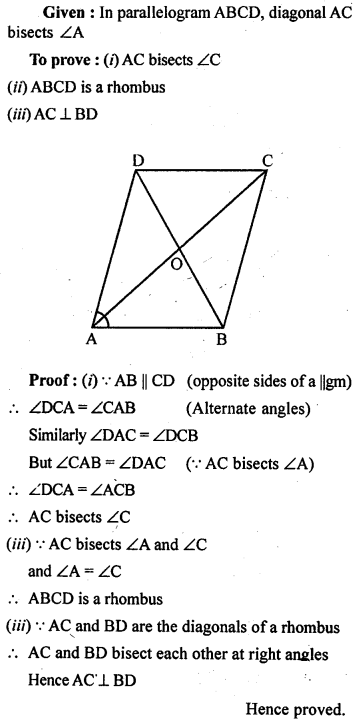
Question 10.
ABCD is a parallelogram. If the diagonal AC bisects ∠A, then prove that:
(i) AC bisects ∠C
(ii) ABCD is a rhombus
(iii) AC ⊥ BD.
Solution:

Question 11.
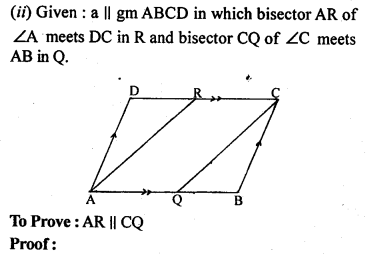
(i) Prove that bisectors of any two adjacent angles of a parallelogram are at right angles.
(ii) Prove that bisectors of any two opposite angles of a parallelogram are parallel.
(iii) If the diagonals of a quadrilateral are equal and bisect each other at right angles, then prove that it is a square.
Solution:

Question 12.
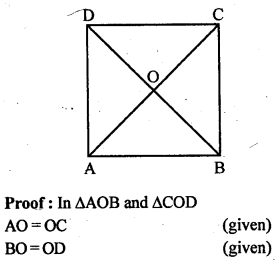
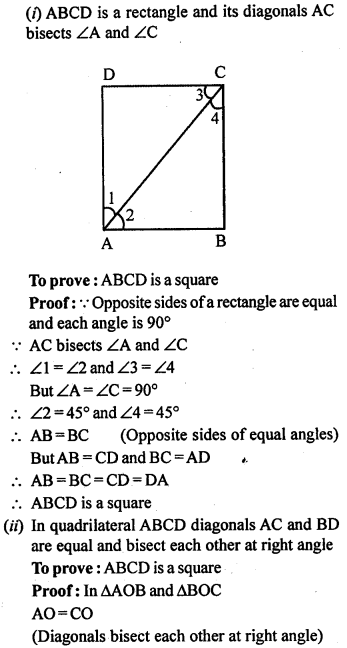
(i) If ABCD is a rectangle in which the diagonal BD bisect ∠B, then show that ABCD is a square.
(ii) Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:

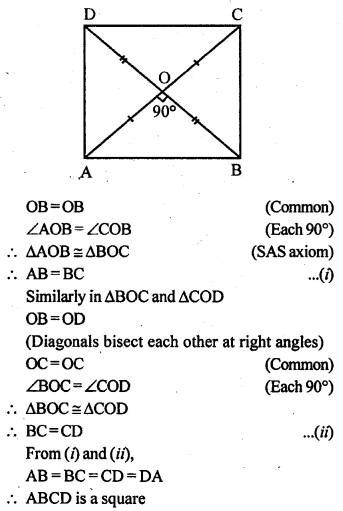
Question 13.
P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
Solution:

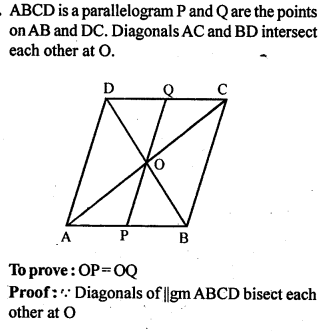
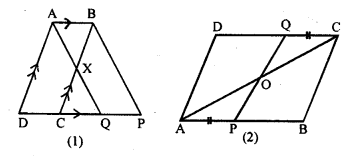
Question 14.
(a) In figure (1) given below, ABCD is a parallelogram and X is mid-point of BC. The line AX produced meets DC produced at Q. The parallelogram ABPQ is completed. Prove that:
(i) the triangles ABX and QCX are congruent;
(ii)DC = CQ = QP
(b) In figure (2) given below, points P and Q have been taken on opposite sides AB and CD respectively of a parallelogram ABCD such that AP = CQ. Show that AC and PQ bisect each other.

Solution:

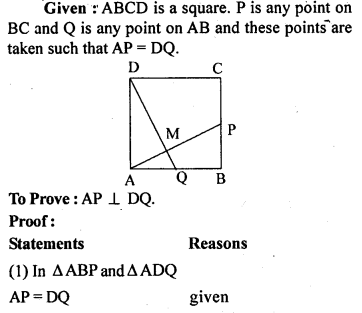
Question 15.
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP=DQ, prove that AP and DQ are perpendicular to each other.
Solution:

Question 16.
If P and Q are points of trisection of the diagonal BD of a parallelogram ABCD, prove that CQ || AP.
Solution:

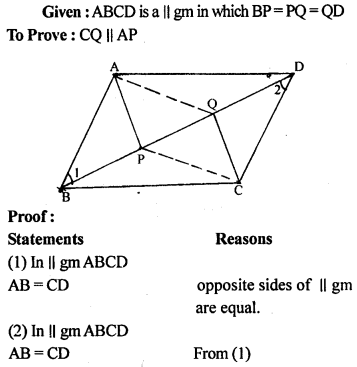
Question 17.
A transversal cuts two parallel lines at A and B. The two interior angles at A are bisected and so are the two interior angles at B ; the four bisectors form a quadrilateral ABCD. Prove that
(i) ABCD is a rectangle.
(ii) CD is parallel to the original parallel lines.

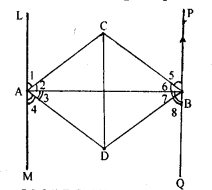
Solution:

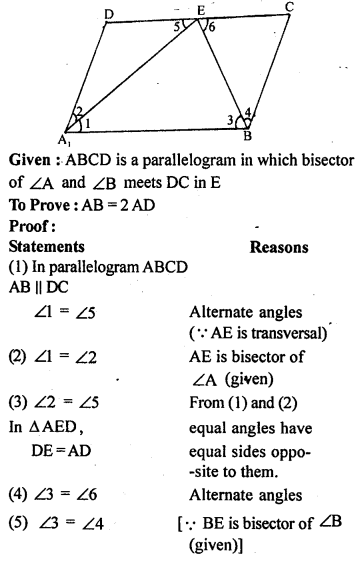
Question 18.
In a parallelogram ABCD, the bisector of ∠A meets DC in E and AB = 2 AD. Prove that
(i) BE bisects ∠B
(ii) ∠AEB = a right angle.
Solution:

Question 19.
ABCD is a parallelogram, bisectors of angles A and B meet at E which lie on DC. Prove that AB
Solution:

Question 20.
ABCD is a square and the diagonals intersect at O. If P is a point on AB such that AO =AP, prove that 3 ∠POB = ∠AOP.
Solution:

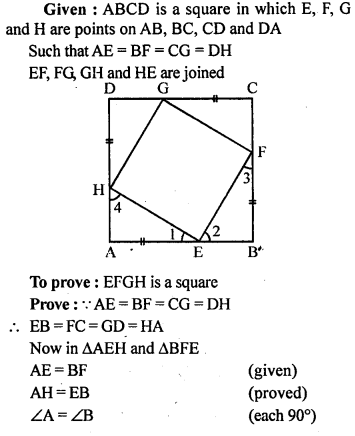
Question 21.
ABCD is a square. E, F, G and H are points on the sides AB, BC, CD and DA respectively such that AE = BF = CG = DH. Prove that EFGH is a square.
Solution:

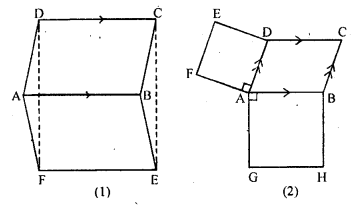
Question 22.
(a) In the Figure (1) given below, ABCD and ABEF are parallelograms. Prove that
(i) CDFE is a parallelogram
(ii) FD = EC
(iii) Δ AFD = ΔBEC.
(b) In the figure (2) given below, ABCD is a parallelogram, ADEF and AGHB are two squares. Prove that FG = AC
Solution:

Question 23.
ABCD is a rhombus in which ∠A = 60°. Find the ratio AC : BD.
Solution:

Exercise 13.2

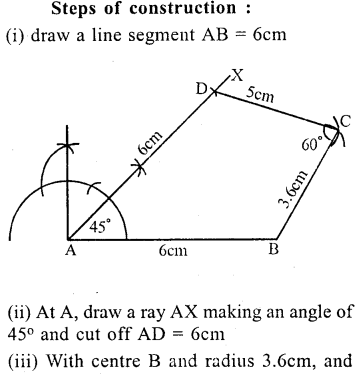
Question 1.
Using ruler and compasses only, construct the quadrilateral ABCD in which ∠ BAD = 45°, AD = AB = 6cm, BC = 3.6cm, CD = 5cm. Measure ∠ BCD.
Solution:

Question 2.
Draw a quadrilateral ABCD with AB = 6cm, BC = 4cm, CD = 4 cm and ∠ ABC = ∠ BCD = 90°
Solution:

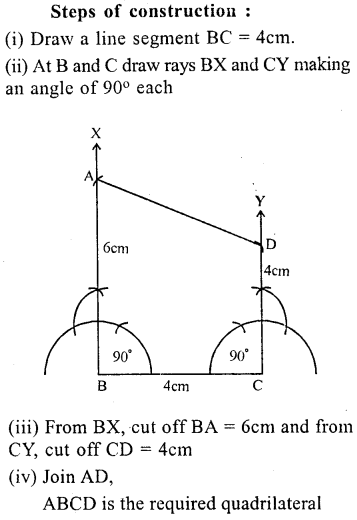
Question 3.
Using ruler and compasses only, construct the quadrilateral ABCD given that AB = 5 cm, BC = 2.5 cm, CD = 6 cm, ∠BAD = 90° and the diagonal AC = 5.5 cm.
Solution:

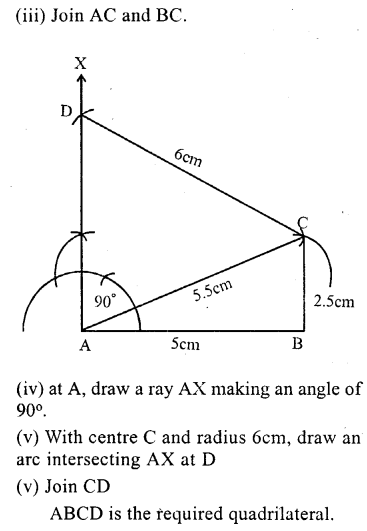
Question 4.
Construct a quadrilateral ABCD in which AB = 3.3 cm, BC = 4.9 cm, CD = 5.8 cm, DA = 4 cm and BD = 5.3 cm.
Solution:

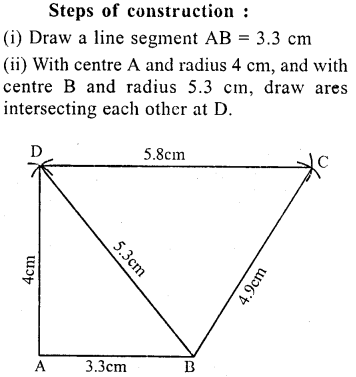
Question 5.
Construct a trapezium ABCD in which AD || BC, AB = CD = 3 cm, BC = 5.2cm and AD = 4 cm
Solution:

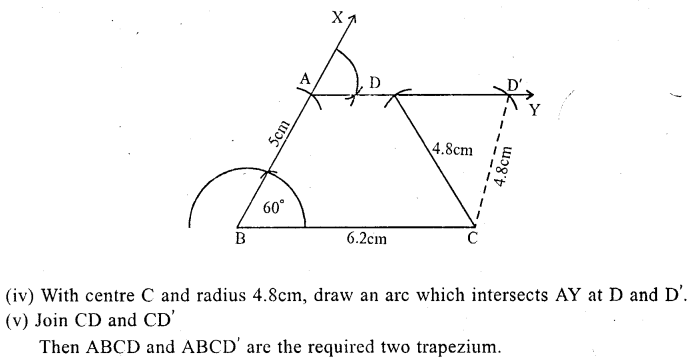
Question 6.
Construct a trapezium ABCD in which AD || BC, ∠B= 60°, AB = 5 cm. BC = 6.2 cm and CD = 4.8 cm.
Solution:

Question 7.
Using ruler and compasses only, construct a parallelogram ABCD with AB = 5.1 cm, BC = 7 cm and ∠ABC = 75°.
Solution:

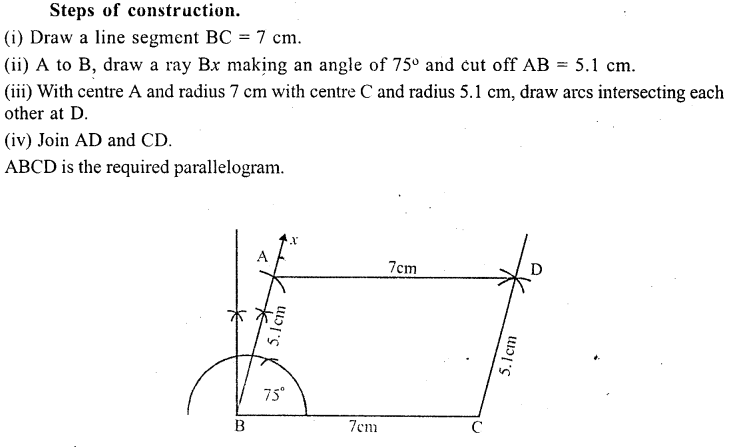
Question 8.
Using ruler and compasses only, construct a parallelogram ABCD in which AB = 4.6 cm, BC = 3.2 cm and AC = 6.1 cm.
Solution:

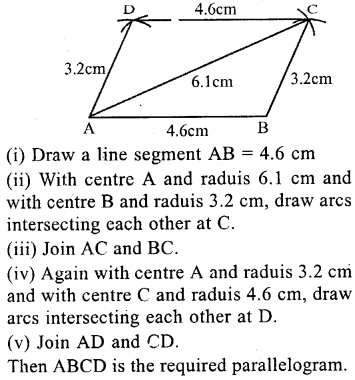
Question 9.
Using ruler and compasses, construct a parallelogram ABCD give that AB = 4 cm, AC = 10 cm, BD = 6 cm. Measure BC.
Solution:

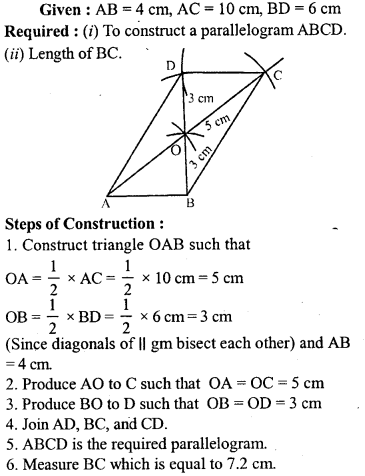
Question 10.
Using ruler and compasses only, construct a parallelogram ABCD such that BC = 4 cm, diagonal AC = 8.6 cm and diagonal BD = 4.4 cm. Measure the side AB.
Solution:

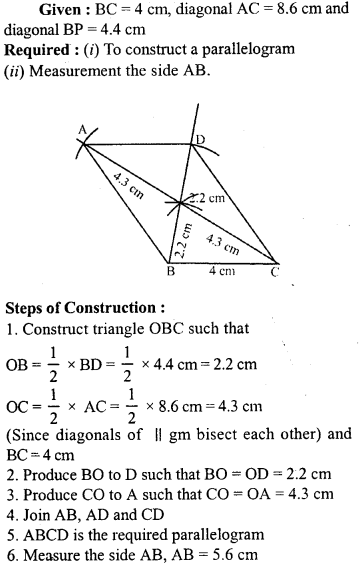
Question 11.
Use ruler and compasses to construct a parallelogram with diagonals 6 cm and 8 cm in length having given the acute angle between them is 60°. Measure one of the longer sides.
Solution:

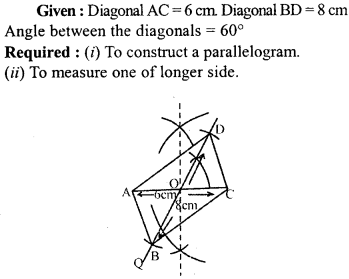
Question 12.
Using ruler and compasses only, draw a parallelogram whose diagonals are 4 cm and 6 cm long and contain an angle of 75°. Measure and write down the length of one of the shorter sides of the parallelogram.
Solution:

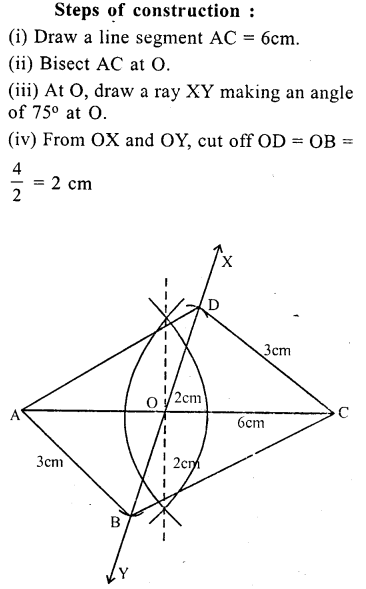
Question 13.
Using ruler and compasses only, construct a parallelogram ABCD with AB = 6 cm, altitude = 3.5 cm and side BC = 4 cm. Measure the acute angles of the parallelogram.
Solution:

Question 14.
The perpendicular distances between the pairs of opposite sides of a parallelogram ABCD are 3 cm and 4 cm and one of its angles measures 60°. Using ruler and compasses only, construct ABCD.
Solution:

Question 15.
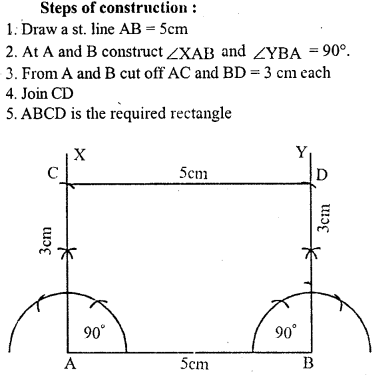
Using ruler and compasses, construct a rectangle ABCD with AB = 5cm and AD = 3 cm.
Solution:

Question 16.
Using ruler and compasses only, construct a rectangle each of whose diagonals measures 6cm and the diagonals intersect at an angle of 45°.
Solution:

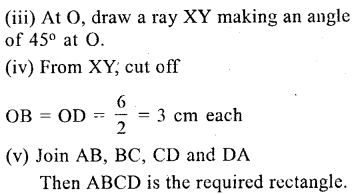
Question 17.
Using ruler and compasses only, construct a square having a diagonal of length 5cm. Measure its sides correct to the nearest millimeter.
Solution:

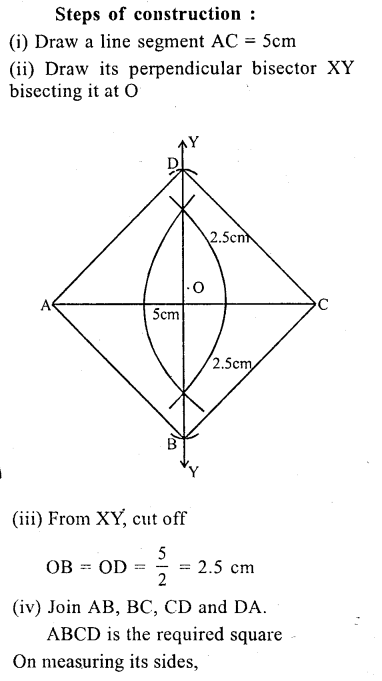
Question 18.
Using ruler and compasses only construct A rhombus ABCD given that AB 5cm, AC = 6cm measure ∠BAD.
Solution:

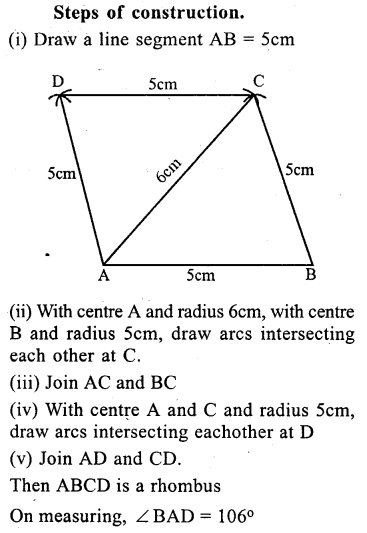
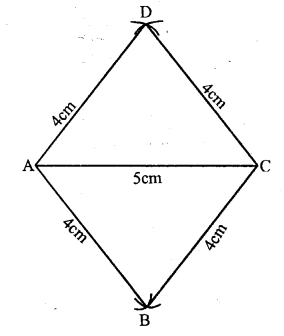
Question 19.
Using ruler and compasses only, construct rhombus ABCD with sides of length 4cm and diagonal AC of length 5 cm. Measure ∠ABC.
Solution:

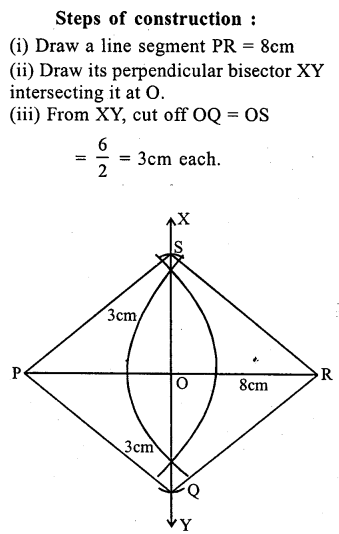
Question 20.
Construct a rhombus PQRS whose diagonals PR and QS are 8cip and 6cm respectively.
Solution:

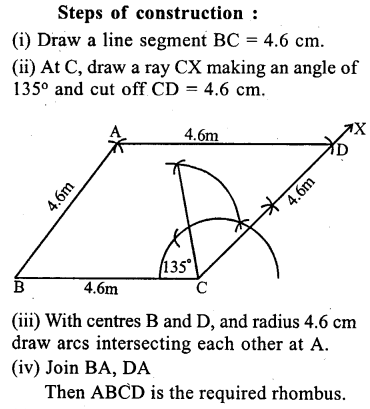
Question 21.
Construct a rhombus ABCD of side 4.6 cm and ∠BCD = 135°, by using ruler and compasses only.
Solution:

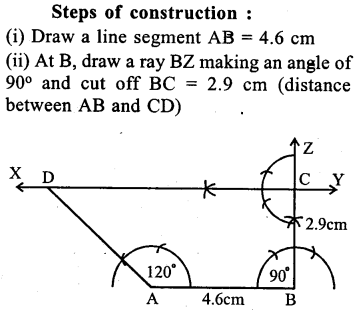
Question 22.
Construct a trapezium in which AB || CD, AB = 4.6 cm, ∠ ABC = 90°, ∠ DAB = 120° and the distance between parallel sides is 2.9 cm.
Solution:

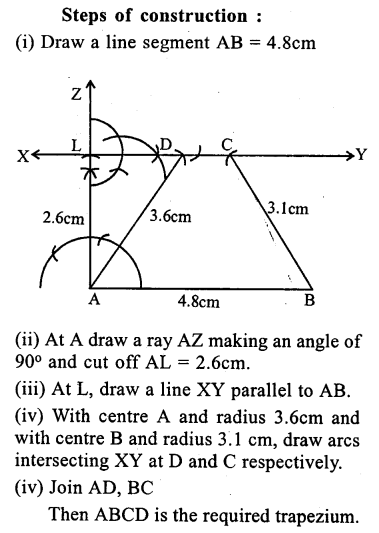
Question 23.
Construct a trapezium ABCD when one of parallel sides AB = 4.8 cm, height = 2.6cm, BC = 3.1 cm and AD = 3.6 cm.
Solution:

Question 24.
Construct a regular hexagon of side 2.5 cm.
Solution:

Multiple Choice Questions

Choose the correct answer from the given four options (1 to 12):
Question 1.
Three angles of a quadrilateral are 75°, 90° and 75°. The fourth angle is
(a) 90°
(b) 95°
(c) 105°
(d) 120°
Solution:
Sum of 4 angles of a quadrilateral = 360° Sum of three angles = 75° + 90° + 75° = 240° Fourth angle = 360° – 240° = 120° (d)

Question 2.
A quadrilateral ABCD is a trapezium if
(a) AB = DC
(b) AD = BC
(c) ∠A + ∠C = 180°
(d) ∠B + ∠C = 180°
Solution:
A quadrilateral ABCD is a trapezium if ∠B + ∠C= 180°
(Sum of co-interior angles) (d)

Question 3.
If PQRS is a parallelogram, then ∠Q – ∠S is equal to
(a) 90°
(b) 120°
(c) 0°
(d) 180°
Solution:
PQRS is a parallelogram ∠Q – ∠S = 0
(∵ Opposite angles of a parallelogram, are equal) (c)

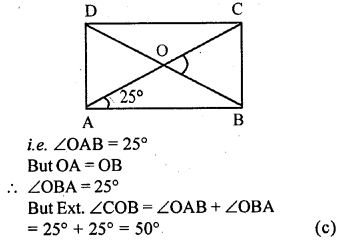
Question 4.
A diagonal of a rectangle is inclined to one side of the rectangle at 25°. The acute angle between the diagonals is
(a) 55°
(b) 50°
(c) 40°
(d) 25°
Solution:
In a rectangle a diagonal is inclined to one side of the rectangle is 25°

Question 5.
ABCD is a rhombus such that ∠ACB = 40°. Then ∠ADB is
(a) 40°
(b) 45°
(c) 50°
(d) 60°
Solution:

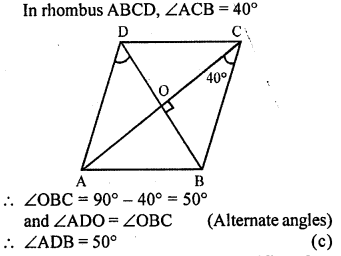
Question 6.
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠D AC = 32° and ∠AOB = 70°, then ∠DBC is equal to
(a) 24°
(b) 86°
(c) 38°
(d) 32°
Solution:

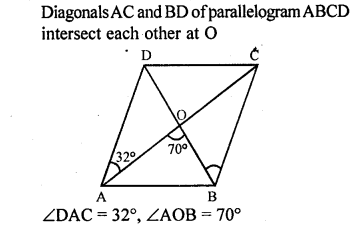
Question 7.
If the diagonals of a square ABCD intersect each other at O, then ∆OAB is
(a) an equilateral triangle
(b) a right angled but not an isosceles triangle
(c) an isosceles but not right angled triangle
(d) an isosceles right angled triangle
Solution:

Question 8.
If the diagonals of a quadrilateral PQRS bisect each other, then the quadrilateral PQRS must be a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) square
Solution:
Diagonals of a quadrilateral PQRS bisect each other, then quadrilateral must be a parallelogram.
(∵ A rhombus, rectangle and square are also parallelogram) (a)

Question 9.
If the diagonals of a quadrilateral PQRS bisect each other at right angles, then the quadrilateral PQRS must be a
(a) parallelogram
(b) rectangle
(c) rhombus
(d) square
Solution:
Diagonals of quadrilateral PQRS bisect each other at right angles, then quadrilateral PQRS [ must be a rhombus.
(∵ Square is also a rhombus with each angle equal to 90°) (c)

Question 10.
Which of the following statement is true for a parallelogram?
(a) Its diagonals are equal.
(b) Its diagonals are perpendicular to each other.
(c) The diagonals divide the parallelogram into four congruent triangles.
(d) The diagonals bisect each other.
Solution:
For a parallelogram an the statement ‘The diagoanls bisect each other’ is true. (d)

Question 11.
Which of the following is not true for a parallelogram?
(a) opposite sides are equal
(b) opposite angles are equal
(c) opposite angles are bisected by the diagonals
(d) diagonals bisect each other
Solution:
The statement that in a parallelogram, .the opposite angles are bisected by the diagonals, is not true in each case. (c)

Question 12.
A quadrilateral in which the diagonals are equal and bisect each other at right angles is a
(a) rectangle which is not a square
(b) rhombus which is not a square
(c) kite which is not a square
(d) square
Solution:
In a quadrilateral, if diagonals are equal and bisect each other at right angles, is a square. (d)

Chapter Test

Question P.Q.
The interior angles of a polygon add upto 4320°. How many sides does the polygon have ?
Solution:

Question P.Q.
If the ratio of an interior angle to the exterior angle of a regular polygon is 5:1, find the number of sides.
Solution:

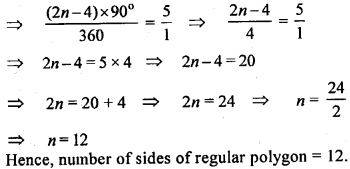
Question P.Q.
In a pentagon ABCDE, BC || ED and ∠B: ∠A : ∠E =3:4:5. Find ∠A.
Solution:

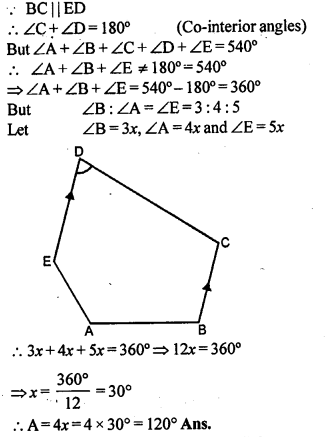
Question 1.
In the given figure, ABCD is a parallelogram. CB is produced to E such that BE=BC. Prove that AEBD is a parallelogram.

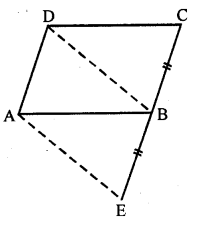
Solution:

Question 2.
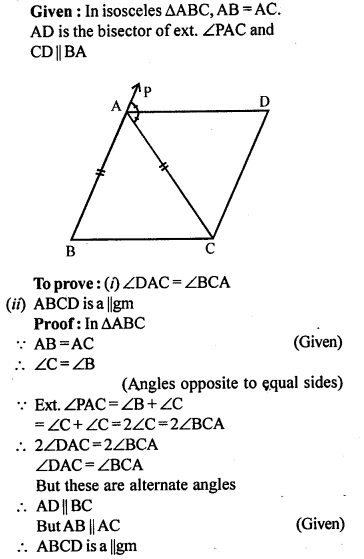
In the given figure, ABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD || BA. Show that
(i) ∠DAC=∠BCA
(ii) ABCD is a parallelogram.
Solution:

Question 3.
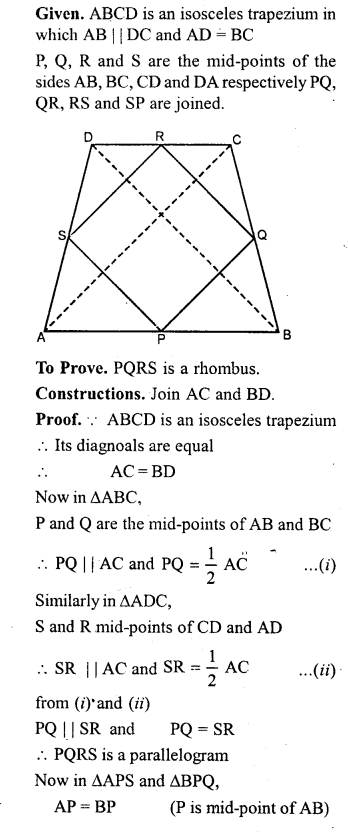
Prove that the quadrilateral obtained by joining the mid-points of an isosceles trapezium is a rhombus.
Solution:

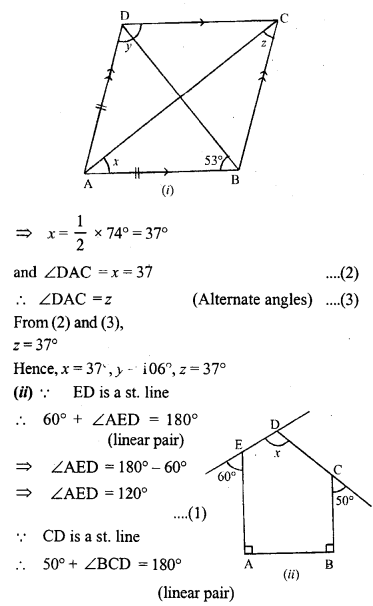
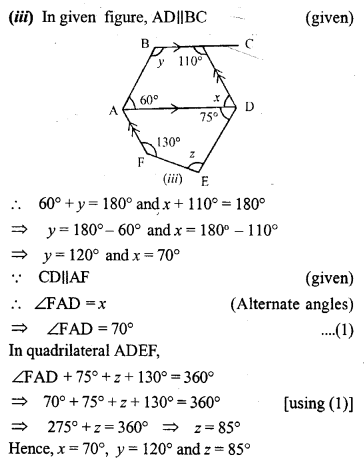
Question 4.
Find the size of each lettered angle in the Following Figures.

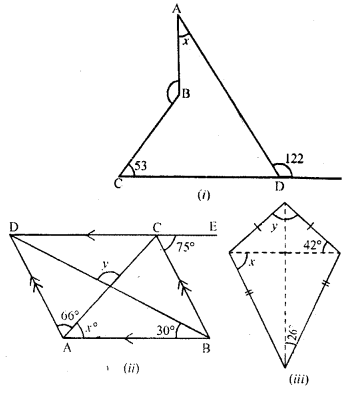
Solution:

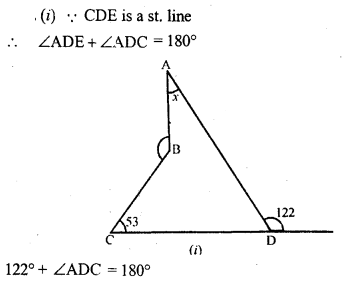
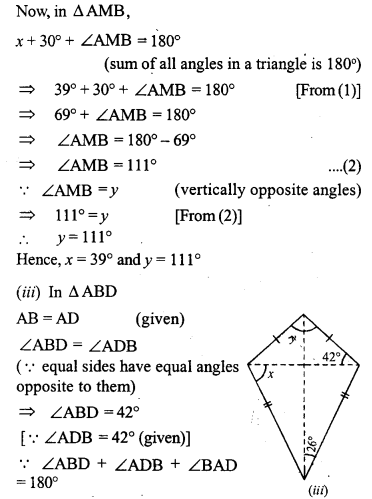
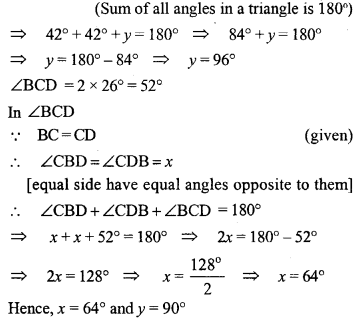
Question 5.
Find the size of each lettered angle in the following figures :

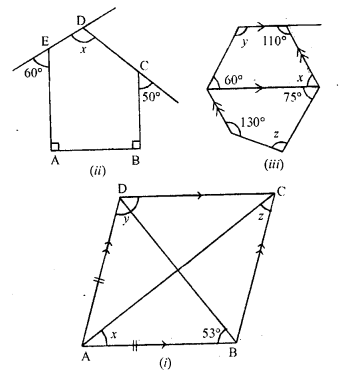
Solution:

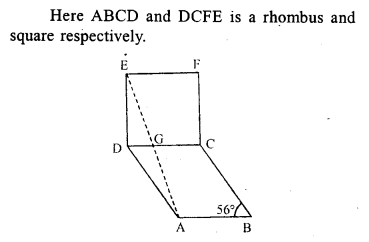
Question 6.
In the adjoining figure, ABCD is a rhombus and DCFE is a square. If ∠ABC = 56°, find
(i) ∠DAG
(ii) ∠FEG
(iii) ∠GAC
(iv) ∠AGC.

Solution:

Question 7.
If one angle of a rhombus is 60° and the length of a side is 8 cm, find the lengths of its diagonals.
Solution:

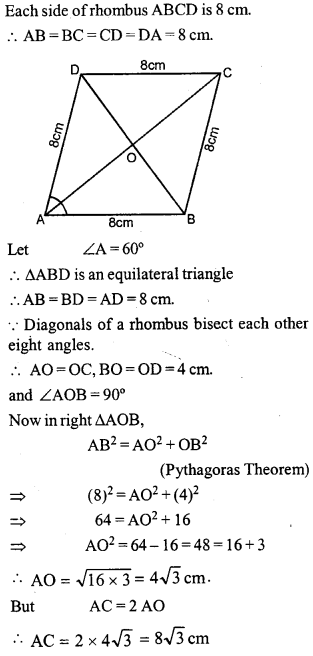
Question 8.
Using ruler and compasses only, construct a parallelogram ABCD with AB = 5 cm, AD = 2.5 cm and ∠BAD = 45°. If the bisector of ∠BAD meets DC at E, prove that ∠AEB is a right angle.
Solution: