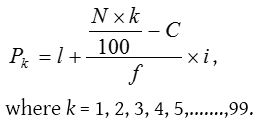How to Find the Median Value
The median is the central value of the set of observations provided all the observations are arranged in the ascending or descending orders. It is generally used, when effect of extreme items is to be kept out.
Example: The median of 10, 14, 11, 9, 8, 12, 6 is
Solution: Arrange the items in ascending order i.e., 6, 8, 9, 10, 11, 12, 14.
If n is odd then, Median = value of \({ \left( \frac { n+1 }{ 2 } \right) }^{ th }\) term
∴ Median = \({ \left( \frac { n+1 }{ 2 } \right) }^{ th }\) term = 4th term = 10.
(1) Calculation of median
(i) Individual series: If the data is raw, arrange in ascending or descending order. Let n be the number of observations.
If n is odd, Median = value of \({ \left( \frac { n+1 }{ 2 } \right) }^{ th }\) term.
If n is even,
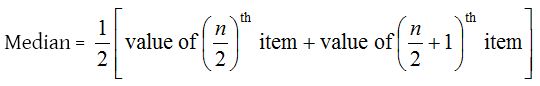
(ii) Discrete series: In this case, we first find the cumulative frequencies of the variables arranged in ascending or descending order and the median is given by Median = \({ \left( \frac { n+1 }{ 2 } \right) }^{ th }\) observation, where n is the cumulative frequency.
(iii) For grouped or continuous distributions: In this case, following formula can be used.
(a) For series in ascending order,
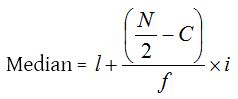
Where l = Lower limit of the median class
f = Frequency of the median class
N = The sum of all frequencies
i = The width of the median class
C = The cumulative frequency of the class preceding to median class.
(b) For series in descending order
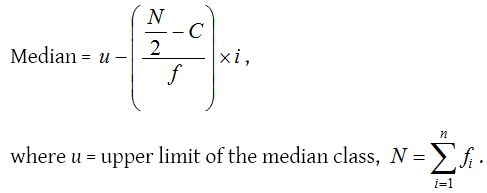
As median divides a distribution into two equal parts, similarly the quartiles, quantiles, deciles and percentiles divide the distribution respectively into 4, 5, 10 and 100 equal parts. The jth quartile is given by
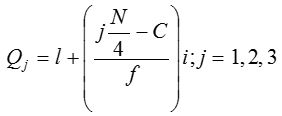
Q1 is the lower quartile, Q2 is the median and Q3 is called the upper quartile.
(2) Lower quartile
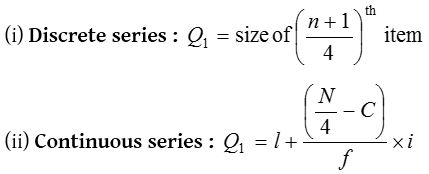
(3) Upper quartile
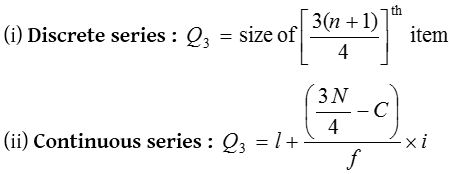
(4) Decile
Decile divide total frequencies N into ten equal parts.
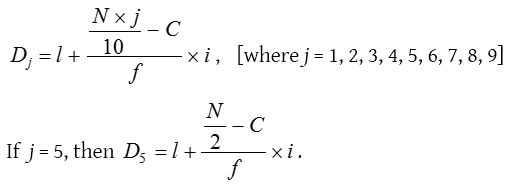
Hence D5 is also known as median.
(5) Percentile
Percentile divide total frequencies N into hundred equal parts and