How do you Measure the Refractive Index?
- The law of refraction states that:
- The incident ray, the refracted ray and the normal all lie in the same plane.
- The ratio of the sine of the angle of incidence, i to the sine of the angle of refraction, r is a constant,
\(\frac{\sin \,i}{\sin \,r}=\text{ constant}\)
- Refractive Index Formula: The value of this constant, \(\frac{\sin \,i}{\sin \,r}\) for a light ray passing through a vacuum into a given medium is called the refractive index, n of the medium. It is defined as:

- This relationship is also known as Snell’s law.
- (a) Refractive Index in terms of Speed of Light:
The refractive index of a medium may be defined in terms of the speed of light as follows
\( \text{Refractive index }=\frac{\text{Speed}\,\,\text{of}\,\,\text{light}\,\,\text{in}\,\,\text{vacuum}}{\text{Speed}\,\,\text{of}\,\,\text{light}\,\,\text{in}\,\,\text{medium}} \)
\( \text{ }\!\!\mu\!\!\text{ }=\frac{c}{v} \)
(b) Refractive Index in terms of Wavelength:
Since the frequency (ν) remains unchanged when light passes from one medium to another, therefore,
\( \text{ }\!\!\mu\!\!\text{ }=\frac{c}{v}=\frac{{{\lambda }_{vac}}\times \nu }{{{\lambda }_{med}}\times \nu }=\frac{{{\lambda }_{vac}}}{{{\lambda }_{med}}} \)
(c) Relative Refractive Index:
The relative refractive index of medium 2 with respect to medium 1 is defined as the ratio of speed of light (ν1) in the medium 1 to the speed of light (ν2) in medium 2 and is denoted by 1µ2. Thus,
\(_{1}{{\text{ }\!\!\mu\!\!\text{ }}_{\text{2}}}=\frac{{{v}_{1}}}{{{v}_{2}}}=\frac{{{\lambda }_{1}}}{{{\lambda }_{2}}}=\frac{{{\mu }_{2}}}{{{\mu }_{1}}}\)
As refractive index is the ratio of two similar physical quantities, so it has no unit and dimension. - Factors On Which The Refractive Index Of A Medium Depends Are:
- Nature of the medium.
- Wavelength of the light used.
- Temperature
- Nature of the surrounding medium.
It may be noted that refractive index is a characteristic of the pair of the media and also depends on the wavelength of light, but is independent of the angle of incidence.
- The angle of refraction of light depends on the refractive index of the mediums and the angle of incidence.
- Figure shows how the angle of refraction, r depends on the angle of incidence, i when light travels from air into three different media. Mediums and media are the plural forms of medium.
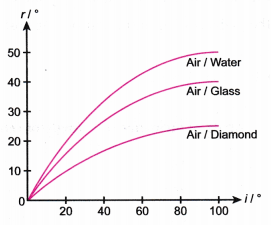
- For a given angle of incidence, i the angle of refraction, r becomes smaller in a denser medium. As the decrease of the speed of light is greater in a denser medium, the light ray will bend more.
- When the angle i and the angle r are expressed as sin i and sin r respectively, their relationship is as shown in Figure.
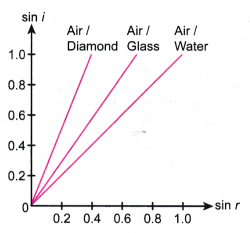
- The gradient of the graph of sin i against sin r shows how much the light is bent in the denser medium. This gradient is the value of the refractive index, n of a medium.
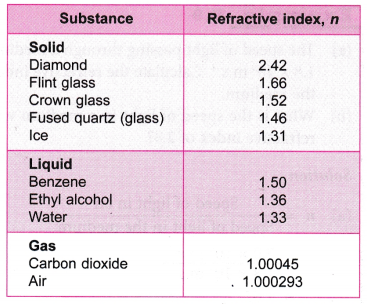
- Table shows the refractive indices of some substances. Substances which are optically denser have a larger refractive index and the light rays bend or refract more in these substance.
People also ask
- What is Refraction of Light?
- Analysing Refraction of Waves
- Examples of refraction of light
- What is the index of refraction?
- What is atmospheric refraction?
- Refraction of light through glass slab
Relation between Refractive Index and Speed of Light
- The speed of light in a vacuum is about 3.0 x 108 m s-1. Light travels much slower in a medium.
- The refraction of light is due to the change of speed when light passes from one medium to another.
- Therefore, the refractive index of a medium may also be defined as the ratio of the speed of light in air or vacuum to the speed of light in that medium. Speed of light in air or vacuum Speed of light in the medium

- Table shows how the refractive index of some materials are related to the speed of light passing through them.
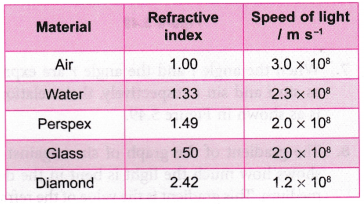
- The higher the refractive index of a medium, the lower will be the speed of light passing through it.
- A medium with a higher refractive index is an optically denser medium.
Refractive Index Example Problems with Solutions
- Figure shows the angle of incidence on an air water boundary.
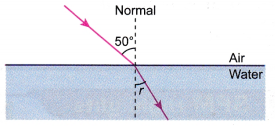
Calculate the angle of refraction, r if the refractive index of water is 1.33.
Solution:
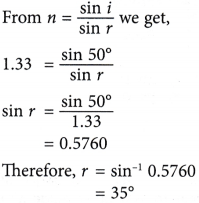
- Figure shows an incident ray in a glass.
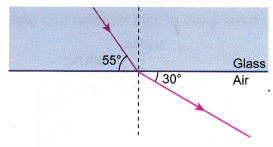
Using the angles shown in the figure, determine the refractive index of the glass.
Solution:
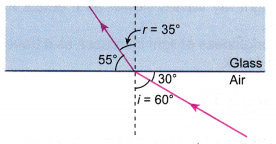
By using the principle of reversibility of light, the angle of incidence, i in air and the angle of refraction, r in glass can be found.
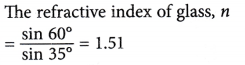
- (a) The speed of light passing through a medium is 1.8 x 108 m s-1. Calculate the refractive index of the medium.
(b) What is the speed of light in a medium with a refractive index of 2.4?
Solution:


Relation between Angle of Incidence and Angle of Refraction Experiment
Aim: To find the relationship between the angle of incidence and the angle of refraction.
Problem: What is the relationship between the angle of incidence and the angle of refraction?
Hypothesis: When the angle of incidence, i increases, the angle of refraction, r also increases.
Variables:
(a) Manipulated variable: Angle of incidence, i
(b) Responding variable: Angle of refraction, r
(c) Fixed variable: Type of glass block
Materials: White paper
Apparatus: Protractor, a pair of compasses, low voltage power supply, ray box with single slit, semicircular glass block, pencil, ruler
Method:
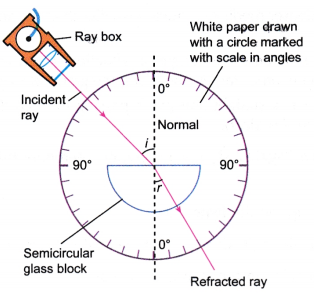
- The apparatus is set up as shown in Figure.
- A semicircular glass block is placed at the centre of a circle marked, on a white paper, with angles as shown.
- A single ray from a ray box is incident at the centre of the semicircular glass block from its flat edge at an
angle of incidence, i = 150. - The angle Of refraction, r is measured and recorded in Table.
- Steps 3 and 4 are repeated with angles of incidence, i = 300, 450, 600, 700 and 800.
- The values of sin i, sin r and \(\frac{\sin \,i}{\sin \,r}\) are calculated and recorded in table.
- The graphs of i against r and sin i against sin r are plotted.
Results:
- Tabulation of results.
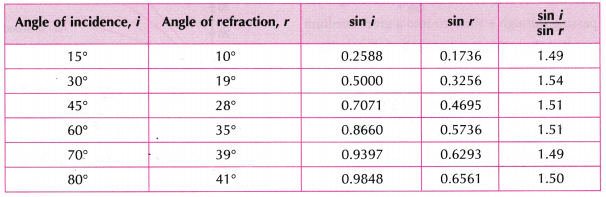
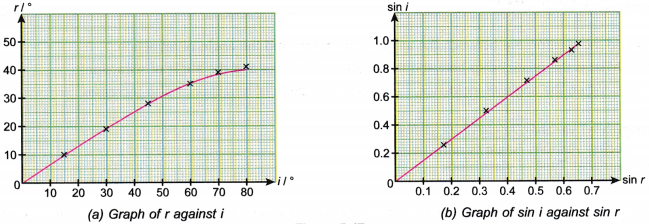
- Graphs of r against i and sin i against sin r.
Discussion:
- The angle of refraction, r in a denser medium is always smaller than the angle of incidence, i in a less dense medium.
- When the angle of incidence, i increases, the angle of refraction, r also increases. The increment in angle r becomes smaller when angle i becomes larger. Therefore, the graph of r against i is not a straight line graph.
- The graph of sin i against sin r is a straight line graph passing through the origin. This shows that sin i is directly proportional to sin r (sin ∝ sin r).
- The gradient of the graph of sin i against sin r is a constant. Therefore, the ratio of \(\frac{\sin \,i}{\sin \,r}\) is a constant.
Conclusions:
- The results of the experiment support the hypothesis.
- The relationship between the angle of incidence, i and the angle of refraction, r is obtained from the ratio of \(\frac{\sin \,i}{\sin \,r}\) which is a constant. This relationship is also known as Snell’s law. The ratio of \(\frac{\sin \,i}{\sin \,r}\) is the refractive index of the medium. In this case, the medium is the glass block.