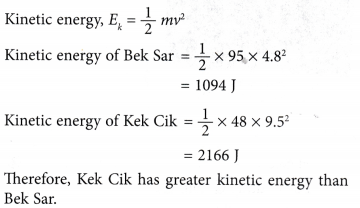What is Kinetic Energy
Kinetic Energy: The energy of a body due to its motion is called kinetic energy. In other words. The ability of a body to do work by virtue of its motion is called its kinetic energy.
Expression for Kinetic Energy: The kinetic energy of a body is measured in terms of the amount of work done by an opposing force that brings the body to rest from its present state of motion.
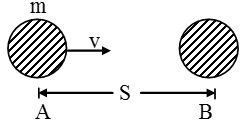
Suppose a body of mass m is moving with a velocity v and is brought to rest by an opposing force F.
Now retarding force is given by
F = ma …(1)
Now using the equation of motion,
v2 – u2 = 2as, we get
02 = v2 – 2as
∴s=\( \frac{{{v}^{2}}}{2a} \) ….. (2)
Kinetic energy of the body = work done by the retarding force
or Kinetic energy = force × displacement
= F . s …(3)
Substituting the value of F from equation (1) and the value of s from equation (2) in equation (3), we get
\( K.E.=ma\times \frac{{{v}^{2}}}{2a} \)
\( K.E.=\frac{1}{2}m{{v}^{2}} \)
Thus, a body of mass m and moving with a velocity v has the capacity of doing work equal to \(\frac { 1 }{ 2 }\) mv2 before it stops.
Kinetic Energy Example Problems With Solutions
Example 1: A bullet of mass 100 gm is fired with a velocity 50 m/s from a gun. Calculate the kinetic energy of the bullet.
Solution: Kinetic energy is given by
\( K.E.=\frac{1}{2}m{{v}^{2}} \)
Here m = 100 gm = 0.1 kg; v = 500 m/s
K.E. = \(\frac { 1 }{ 2 }\) × 0.1 × (50)2
= \(\frac { 1 }{ 2 }\) × 0.1 × 50 × 50 = 125 J
Example 2: A 4 kg body is dropped from the top of a building of height 2.5 m. With what velocity will it strike the ground ? What is its kinetic energy when it strikes the ground ?
(Takes g = 9.8 m/s2)
Solution: Velocity of the body with which it strikes the ground can be calculated by using the equation, v2 = u2 + 2gh
Here u = 0; g = 9.8 m/s2 ; h = 2.5 m
Substituting these values, we get
v2 = 02 + 2 × 9.8 × 2.5 = 49
or v = 7 m/s
Thus, the speed of the body with which it strikes the ground = 7 m/s.
Example 3: Calculate the velocity of 4 kg mass with kinetic energy of 128 J.
Solution: The formula for kinetic energy is given by
\( K.E.=\frac{1}{2}m{{v}^{2}} \)
Here K.E. = 128 J; m = 4 kg
128 = \(\frac { 1 }{ 2 }\) × 4 × v2
v2 = 64
v = 8 m/s
Example 4: Which would have a greater effect on the kinetic energy of an object, doubling the mass or doubling the velocity ?
Solution: (i) The kinetic energy of a body is directly proportional to its “mass” (m). So, if we double the mass (so that it becomes 2m), then the kinetic energy will also get doubled.
(ii) On the other hand, kinetic energy of a body is directly proportional to the “square of its velocity” (v2). So, if we double the velocity (so that it becomes 2v), then the kinetic energy will become four times. This is because : (2v)2 = 4v2.
It is clear from the above discussion that doubling the velocity has a greater effect on the kinetic energy of an object.
Example 5: Two bodies of equal masses move with uniform velocity v and 3v respectively. Find the ratio of their kinetic energies.
Solution: In this problem, the masses of the bodies are equal, so let the mass of each body be m. We will now write down the expression for the kinetic energies of both the bodies separately.
(i) Mass of first body = m
Velocity of first body = v
So, K.E. of first body = \(\frac { 1 }{ 2 }\) mv2 ….. (1)
(ii) Mass of second body = m
Velocity of second body = 3v
So, K.E. of second body = \(\frac { 1 }{ 2 }\) m (3v)2
= \(\frac { 1 }{ 2 }\) m × 9 v2
= \(\frac { 9 }{ 2 }\) mv2 ….. (2)
Now, to find out the ratio of kinetic energies of the two bodies, we should divide equation (1) by equation (2), so that
\( \frac{\text{K}\text{.E}\text{.}\,\text{of}\,\text{first}\,\text{body}}{\text{K}\text{.E}\text{.}\,\text{of}\,\text{sec}\,\text{ondbody}\,}=\frac{\frac{\text{1}}{\text{2}}\text{m}{{\text{v}}^{\text{2}}}}{\frac{\text{9}}{\text{2}}\text{m}{{\text{v}}^{\text{2}}}} \)
\( \frac{\text{K}\text{.E}\text{.}\,\text{of}\,\text{first}\,\text{body}}{\text{K}\text{.E}\text{.}\,\text{of}\,\text{sec}\,\text{ond}\,\text{body}}=\frac{\text{1}}{\text{9}}\text{ }….\text{ (3)} \)
Thus, the ratio of the kinetic energies is 1 : 9. We can also write down the equation (3) as follows:
K.E. of second body = 9 × K.E. of first body
That is, the kinetic energy of second body is 9 times the kinetic energy of the first body. It is clear from this example that when the velocity (or speed) of a body is “tripled” (from v to 3v), then its kinetic energy becomes “nine times”.
Example 6. What is the kinetic energy of a 1200 kg car travelling at a velocity of 25 m s-1?
Solution:
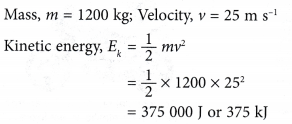
Example 7. Table shows the masses and velocities of two boys, Bek Sar and Kek Cik respectively.
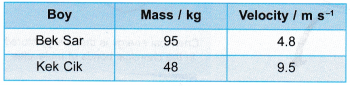
Which of the boys has greater kinetic energy?
Solution: