Earth’s Gravitational Force
- The force which earth exerts on a body is called ‘force of gravity’. i.e.
\(F=\frac{GMm}{{{R}^{2}}}\)
Where M = mass of the earth, R = radius of the earth. - Due to this force, a body released from some height on the earth’s surface falls towards the earth with its velocity increasing at a constant rate.
Acceleration due to Gravity:
- The acceleration produced in a body due to attraction of earth is called the acceleration due to gravity and is denoted by ‘g’.
- \( g=\frac{GM}{{{R}^{2}}}=9.8\text{ m/}{{\text{s}}^{\text{2}}} \\ \)
near the earth surface - \( \text{g on moon }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\approx \frac{{{g}_{e}}}{6}=\frac{9.8}{6}\text{m/}{{\text{s}}^{\text{2}}} \)
- A body moving upwards with some initial velocity, experiences a retardation of 9.8 m/s2 & its velocity decreases continuously unless it becomes zero.
- After this, it again starts falling towards the earth with the same acceleration of 9.8 m/s2.
- The value of g is minimum at equator and maximum at poles.
- The value of g does not depend upon the mass of the body falling towards the earth.
Variation In The Value Of Gravitational Acceleration (g)
(A) Variation with altitude or height:
- When a body moves above the earth’s surface the distance of the body from the centre of earth increases there by decreasing the force of attraction.
- At the earth’s surface
\( \text{g}=\frac{\text{GM}}{{{\text{R}}^{\text{2}}}} \) - At a height h above the earth’s surface
\( \text{g}=\frac{\text{GM}}{{{\text{(R + h)}}^{\text{2}}}} \)
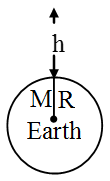
- As we go above the earth’s surface the value of g goes on decreasing.
(B) Variation with depth d:
- As we go deeper inside the earth, the body gets attracted by the core of the earth which is smaller in mass.
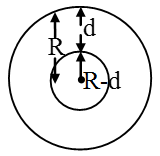
- As we go inside the earth, the value of g decreases.
- Force of attraction decreases and thus decreasing the value of g and becoming zero at the centre.
(C) Variation due to rotation of the earth:
Due to the rotation of the earth, the weight of a body is maximum at the poles and minimum at the equator.
Difference Between Mass and Weight
Mass | Weight | |
1. | Mass of a body is defined as the quantity of matter contained in it. | Weight of a body is the force with which it is attracted towards the centre of the earth. W = mg |
2. | Mass of a body remains constant and does not change from place to place. | Weight of a body changes from place to place. It depends upon the value of g. Weight of a body on another planet will be different. |
3. | Mass is measured by a pan balance. | Weight is measured by a spring balance. |
4. | Unit of mass is kg. | Unit of weight is newton or kg-wt. |
5. | Mass of a body cannot be zero. | Weight of a body can be zero. Ex. astronauts experience weightlessness in spaceships. |
6. | Mass is a scalar quantity. | Weight is a vector quantity. |
Earth’s Gravitational Force Example Problems With Solutions
Example 1: Given mass of earth is 6 × 1024 kg and mean radius of earth is 6.4 × 106 m. Calculate the value of acceleration due to gravity (g) on the surface of the earth.
Solution: The formula for the acceleration due to gravity is given by
\( \text{g}=\frac{\text{GM}}{{{\text{R}}^{\text{2}}}} \)
Here, G = 6.67 × 10–11 Nm2/kg2;
M = mass of earth = 6 × 1024 kg;
R = radius of earth = 6.4 × 106 m
\(g=\frac{6.67\times {{10}^{-11}}\times 6\times {{10}^{24}}}{{{(6.4\times {{10}^{6}})}^{2}}}\)
g = 9.8 m/s2
Example 2: Calculate the value of acceleration due to gravity on a planet whose mass is 4 times as that of the earth and radius is 3 times as that of the earth.
Solution: If M is the mass of the earth and R is the radius of earth, the value of acceleration due to gravity on the earth (ge) is given by
\( {{g}_{e}}=\frac{GM}{{{R}^{2}}}\text{ }…..\text{ (1)} \)
Let us consider a planet such that mass of the planet is equal to 4 times the mass of earth. Mp = 4M
Radius of the planet is equal to 3 times the radius of earth.
Re = 3R
Then, acceleration due to gravity on this planet(gp) is
\( {{g}_{e}}=\frac{G\times (4M)}{{{(3R)}^{2}}}=\frac{4}{9}.\frac{GM}{{{R}^{2}}}\text{ }…..\text{ (2)} \)
Dividing equation (2) by equation (1), we get
\( \frac{{{g}_{p}}}{{{g}_{e}}}=\frac{\frac{4}{9}\times \frac{GM}{{{R}^{2}}}}{\frac{GM}{{{R}^{2}}}} \)
\( \frac{{{g}_{p}}}{{{g}_{e}}}=\frac{4}{9} \)
\( {{g}_{p}}=\frac{4}{9}{{g}_{e}} \)
Since ge = 9.8 m/s2
\( {{g}_{p}}=\frac{4}{5}\times 9.8=4.35\text{ m/}{{\text{s}}^{\text{2}}} \)
Thus, acceleration due to gravity on the given planet is 4.35 m/s2.
Example 3: Given the mass of the moon = 7.35 × 1022 kg and the radius of the moon = 1740 km. Calculate the acceleration experienced by a particle on the surface of the moon due to the gravitational force of the moon. Find the ratio of this acceleration to that experienced by the same particle on the surface of the earth.
Solution: If Mm is the mass of the moon and Rm is its radius, then the acceleration experienced by a body on its surface is given by
\( a=\frac{G{{M}_{m}}}{R_{m}^{2}} \)
Here, Mm = 7.3 × 1022 kg;
Rm = 1740 km = 1.74 × 106 m
\( \therefore a=\frac{6.67\times {{10}^{-11}}\times 7.3\times {{10}^{22}}}{{{(1.74\times {{10}^{6}})}^{2}}}=1.57\text{ m/}{{\text{s}}^{\text{2}}} \)
While the acceleration due to gravity on the surface of the earth, is given by
\( {{g}_{e}}=\frac{G{{M}_{e}}}{R_{e}^{2}}=\frac{6.67\times {{10}^{-11}}\times 6\times {{10}^{24}}}{{{(6.4\,\times \,{{10}^{6}})}^{2}}}=9.8\text{ }m/{{s}^{2}} \)
Comparing acceleration due to gravity on moon to that on the earth is
\( \frac{a}{g}=\frac{1.57}{9.8}=0.16 \)
Example 4: At what height above the earth’s surface the value of g will be half of that on the earth’s surface ?
Solution: We know that the value of g at earth’s surface is
\( g=\frac{GM}{{{R}^{2}}}\text{ }…..\text{ (1)} \)
While the value of g at a height h above the earth’s surface is given by
\( g\acute{\ }=\frac{GM}{{{(R+h)}^{2}}}\text{ }…..\text{ (2)} \)
Dividing equation (2) by equation (1), we get
\( \frac{g’}{g}={{\left( \frac{R}{R+h} \right)}^{2}}\text{ or }g\acute{\ }=g{{\left( \frac{R}{R+h} \right)}^{2}} \)
\( \text{Here},\text{ }g\acute{\ }=~\frac{g}{2} \)
\( \therefore \text{ }\frac{g}{2}=g{{\left( \frac{R}{R+h} \right)}^{2}} \)
\( \frac{R+h}{R}=\sqrt{2}R \)
or R + h = √2 R
or h = ( √2 – 1)R
or h = (1.41 – 1) × 6400 = 0.41 × 6400
= 2624 km
Example 5: Given mass of the planet Mars is 6 × 1023 kg and radius is 4.3 × 106 m. Calculate the weight of a man whose weight on earth is 600 N. (Given g on earth = 10 m/s2)
Solution: Weight of the man on earth, W = mg
or 600 = m × 10 or m = 60 kg
So the mass of the man is 60 kg which will remain the same everywhere.
Now acceleration due to gravity on Mars,
\( {{g}_{m}}=\frac{G{{M}_{m}}}{R_{m}^{2}} \)
Here, Mm = 6 × 1023 kg; Rm = 4.3 × 106m
\( \therefore \text{ }{{g}_{m}}=\frac{6.67\times {{10}^{-11}}\times 6\times {{10}^{23}}}{{{(4.3\times {{10}^{6}})}^{2}}} \)
gm = 2.17 m/s2
Now, weight of the man on Mars will be
Wm = m × gm = 60 × 2.17 = 130.2 N