Cross Multiplication Method For Solving Equations

By the method of elimination by substitution, only those equations can be solved, which have unique solution. But the method of cross multiplication discussed below is applicable in all the cases; whether the system has a unique solution, no solution or infinitely many solutions.
Let us solve the following system of equations
a1x + b1y + c1 = 0 ….(1)
a2x + b2y + c2 = 0 ….(2)
Multiplying equation (1) by b2 and equation (2) by b1, we get
a1b2x + b1b2y + b2c1 = 0 ….(3)
a2b1x + b1b2y + b1c2 = 0 ….(4)
Subtracting equation (4) from equation (3), we get
(a1b2 – a2b1) x + (b2c1 – b1c2) = 0
\(\Rightarrow x=\frac{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\)
\(\left[ {{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}\ne 0\text{ and }\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}} \right]\)
\(\text{Similarly, }y=\frac{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\)
These values of x and y can also be written as
\(\frac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\frac{-y}{{{a}_{1}}{{c}_{2}}-{{a}_{2}}{{c}_{1}}}=\frac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\)
Cross Multiplication Method Examples
Example 1: Solve the following system of equations by cross-multiplication method.
2x + 3y + 8 = 0
4x + 5y + 14 = 0
Sol. The given system of equations is
2x + 3y + 8 = 0
4x + 5y + 14 = 0
By cross-multiplication, we get

\(\Rightarrow \frac{x}{3\times 14-5\times 8}=\frac{x}{3\times 14-5\times 8}=\frac{1}{2\times 5-4\times 3}\)
\(\Rightarrow \frac{x}{42-40}=\frac{-y}{28-32}=\frac{1}{10-12} \)
\(\Rightarrow \frac{x}{2}=\frac{-y}{-4}=\frac{1}{-2} \)
\(\Rightarrow \frac { x }{ 2 }\) = \(\frac { -1 }{ 2 }\)
⇒ x = – 1
\(\Rightarrow \frac { -y }{ -4 }\) = \(\frac { -1 }{ 2 }\)
⇒ y = – 2
Hence, the solution is x = – 1, y = – 2
We can verify the solution.
Example 2: Solve the follownig system of equations by the method of cross-multiplication.
2x – 6y + 10 = 0
3x – 7y + 13 = 0
Sol. The given system of equations is
2x – 6y + 10 = 0 ….(1)
3x – 7y + 13 = 0 ….(2)
Using formula for cross multiplication method:
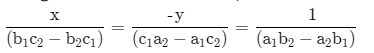
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{x}{-6\times 13-(-7)\times 10}=\frac{-y}{2\times 13-3\times 10}=\frac{1}{2\times (-7)-3\times (-6)} \)
\(\Rightarrow \frac{x}{78+70}=\frac{-y}{26-30}=\frac{1}{-14+18} \)
\(\Rightarrow \frac{x}{-8}=\frac{-y}{-4}=\frac{1}{4} \)
\(\Rightarrow \frac { x }{ -8 }\) = \(\frac { 1 }{ 4 }\)
⇒ x = – 2
\(\Rightarrow \frac { -y }{ -4 }\) = \(\frac { 1 }{ 4 }\)
⇒ y = 1
Hence, the solution is x = – 2, y = 1
Example 3: Solve the following system of equations by the method of cross-multiplication.
11x + 15y = – 23; 7x – 2y = 20
Sol. The given system of equations is
11x + 15y + 23 = 0
7x – 2y – 20 = 0
Using formula for cross multiplication method:
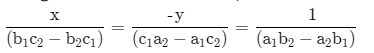
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{x}{15\times (-20)-(-2)\times 23}=\frac{-y}{11\times (-20)-7\times 23}=\frac{1}{11\times (-2)-7\times 15}\)
\(\Rightarrow \frac{x}{-300+46}=\frac{-y}{-220-161}=\frac{1}{-22-105} \)
\(\Rightarrow \frac{x}{-254}=\frac{-y}{-381}=\frac{1}{-127} \)
\(\Rightarrow \frac{x}{-254}=\frac{1}{-127}\Rightarrow x=2 \)
\(\text{and}\frac{-y}{-381}=\frac{1}{-127}\Rightarrow \text{y}=\text{ }-3 \)
Hence, x = 2, y = – 3 is the required solution.
Example 4: Solve the following system of equations by cross-multiplication method.
ax + by = a – b; bx – ay = a + b
Sol. Rewriting the given system of equations, we get
ax + by – (a – b) = 0
bx – ay – (a + b) = 0
Using formula for cross multiplication method:
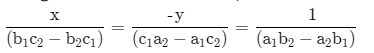
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{x}{b\times \{-(a+b)\}-(-a)\times \{-(a-b)\}}=\frac{-y}{-a(a+b)+b(a-b)}=\frac{1}{-{{a}^{2}}-{{b}^{2}}} \)
\(\Rightarrow \frac{x}{-ab-{{b}^{2}}-{{a}^{2}}+ab}=\frac{-y}{-{{a}^{2}}-ab+ab-{{b}^{2}}}=\frac{1}{-({{a}^{2}}+{{b}^{2}})} \)
\(\Rightarrow \frac{x}{-({{a}^{2}}+{{b}^{2}})}=\frac{-y}{-({{a}^{2}}+{{b}^{2}})}=\frac{1}{-({{a}^{2}}+{{b}^{2}})} \)
\(\Rightarrow \frac{x}{-({{a}^{2}}+{{b}^{2}})}\frac{1}{-({{a}^{2}}+{{b}^{2}})}\Rightarrow x=1 \)
\(and\text{ }\frac{-y}{-({{a}^{2}}+{{b}^{2}})}\frac{1}{-({{a}^{2}}+{{b}^{2}})}\Rightarrow y=-1 \)
Example 5: Solve the following system of equations by cross-multiplication method.
x + y = a – b; ax – by = a2 + b2
Sol. The given system of equations can be rewritten as:
x + y – (a – b) = 0
ax – by – (a2 + b2) = 0
Using formula for cross multiplication method:
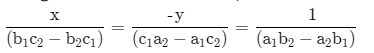
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{x}{-({{a}^{2}}+{{b}^{2}})-(-b)\times \{-(a-b)\}}=\frac{-y}{-({{a}^{2}}+{{b}^{2}})-a\times \{-(a-b)\}}=\frac{1}{-b-a} \)
\(\Rightarrow \frac{x}{-({{a}^{2}}+{{b}^{2}})-b(a-b)}=\frac{-y}{-({{a}^{2}}+{{b}^{2}})+a(a-b)}=\frac{1}{-(b+a)} \)
\(\Rightarrow \frac{x}{-{{a}^{2}}-{{b}^{2}}-ab+{{b}^{2}}}=\frac{-y}{-{{a}^{2}}-{{b}^{2}}+{{a}^{2}}-ab}=\frac{1}{-(a+b)} \)
\(\Rightarrow \frac{x}{-a(a+b)}=\frac{-y}{-b(a+b)}=\frac{1}{-(a+b)} \)
\(\Rightarrow \frac{x}{-a(a+b)}=\frac{1}{-(a+b)}\Rightarrow x=a \)
\(and\text{ }\frac{-y}{-b(a+b)}=\frac{1}{-(a+b)}\Rightarrow y=-b \)
Example 6: Solve the following system of equations by the method of cross-multiplication:
\(\frac{x}{a}+\frac{y}{b}=a+b \) ; \(\frac{x}{{{a}^{2}}}+\frac{y}{{{b}^{2}}}=2 \)
Sol: The given system of equations is rewritten as:
\(\frac{x}{a}+\frac{y}{b}-\left( a+b \right)\) ….(1)
\(\frac{x}{{{a}^{2}}}+\frac{y}{{{b}^{2}}}-2 \) ….(2)
Multiplying equation (1) by ab, we get
bx + ay – ab (a + b) = 0 ….(3)
Multiplying equation (2) by a2 b2, we get
b2x + a2y – 2a2b2 = 0 ….(4)
Using formula for cross multiplication method:
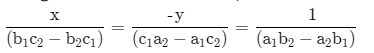
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{x}{-2{{a}^{3}}{{b}^{2}}+{{a}^{3}}b(a+b)}=\frac{-y}{-2{{a}^{2}}{{b}^{3}}+a{{b}^{3}}(a+b)}=\frac{1}{{{a}^{2}}b-a{{b}^{2}}} \)
\(\Rightarrow \frac{x}{-2{{a}^{3}}{{b}^{2}}+{{a}^{4}}b+{{a}^{3}}{{b}^{2}}}=\frac{y}{-2{{a}^{2}}{{b}^{3}}+{{a}^{2}}{{b}^{3}}+a{{b}^{4}}}=\frac{1}{ab(a-b)} \)
\(\Rightarrow \frac{x}{{{a}^{4}}b-{{a}^{3}}{{b}^{2}}}=\frac{-y}{a{{b}^{4}}-{{a}^{2}}{{b}^{3}}}=\frac{1}{ab(a-b)} \)
\(\Rightarrow \frac{x}{{{a}^{3}}b(a-b)}=\frac{y}{a{{b}^{3}}(a-b)}=\frac{1}{ab(a-b)} \)
\(\Rightarrow \frac{x}{{{a}^{3}}b(a-b)}=\frac{1}{ab(a-b)} \)
\(\Rightarrow x=\frac{{{a}^{3}}b(a-b)}{ab(a-b)}={{a}^{2}} \)
\(And\text{ }\frac{y}{a{{b}^{3}}(a-b)}=\frac{1}{ab(a-b)} \)
\(\Rightarrow y=\frac{a{{b}^{3}}(a-b)}{ab(a-b)}={{b}^{2}} \)
Hence, the solution x = a2, y = b2
Example 7: Solve the following system of equations by cross-multiplication method –
ax + by = 1; bx + ay = \(\frac{{{(a+b)}^{2}}}{{{a}^{2}}+{{b}^{2}}}-1\)
Sol: The given system of equations can be written as
ax + by – 1 = 0 ….(1)
\(bx+ay=\frac{{{(a+b)}^{2}}}{{{a}^{2}}+{{b}^{2}}}-1 \)
\(\Rightarrow bx+ay=\frac{{{a}^{2}}+2ab+{{b}^{2}}-{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}} \)
\(\Rightarrow bx+ay=\frac{2ab}{{{a}^{2}}+{{b}^{2}}} \)
\(\Rightarrow bx+ay-\frac{2ab}{{{a}^{2}}+{{b}^{2}}}=0 \) ….. (2)
Rewritting the equations (1) and (2), we have
ax + by – 1 = 0
\(\Rightarrow bx+ay-\frac{2ab}{{{a}^{2}}+{{b}^{2}}}=0 \)
Using formula for cross multiplication method:
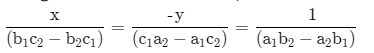
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{x}{b\times \left( \frac{-2ab}{{{a}^{2}}+{{b}^{2}}} \right)-a\times (-1)}=\frac{-y}{a\times \left( \frac{-2ab}{{{a}^{2}}+{{b}^{2}}} \right)-b\times (-1)}=\frac{1}{a\times a-b\times b} \)
\(\Rightarrow \frac{x}{-\frac{2a{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}+a}=\frac{-y}{\frac{-2{{a}^{2}}b}{{{a}^{2}}+{{b}^{2}}}+b}=\frac{1}{{{a}^{2}}-{{b}^{2}}} \)
\(\Rightarrow \frac{x}{\frac{-2a{{b}^{2}}+{{a}^{3}}+a{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}}=\frac{-y}{\frac{-2{{a}^{2}}b+{{a}^{2}}b+{{b}^{3}}}{{{a}^{2}}+{{b}^{2}}}}=\frac{1}{{{a}^{2}}-{{b}^{2}}} \)
\(\Rightarrow \frac{x}{\frac{a({{a}^{2}}-{{b}^{2}})}{{{a}^{2}}+{{b}^{2}}}}=\frac{-y}{\frac{b({{b}^{2}}-{{a}^{2}})}{{{a}^{2}}+{{b}^{2}}}}=\frac{1}{{{a}^{2}}-{{b}^{2}}} \)
\( \Rightarrow \frac{x}{\frac{a({{a}^{2}}-{{b}^{2}})}{{{a}^{2}}+{{b}^{2}}}}=\frac{1}{{{a}^{2}}-{{b}^{2}}}\Rightarrow x=\frac{a}{{{a}^{2}}+{{b}^{2}}} \)
\(and\text{ }\frac{-y}{\frac{b({{b}^{2}}-{{a}^{2}})}{{{a}^{2}}+{{b}^{2}}}}=\frac{1}{{{a}^{2}}-{{b}^{2}}}\Rightarrow y=\frac{b}{{{a}^{2}}+{{b}^{2}}} \)
Hence, the solution is \(x=\frac{a}{{{a}^{2}}+{{b}^{2}}},y=\frac{b}{{{a}^{2}}+{{b}^{2}}} \)
Example 8: Solve the following system of equations in x and y by cross-multiplication method
(a – b) x + (a + b) y = a2 – 2ab – b2
(a + b) (x + y) = a2 + b2
Sol: The given system of equations can be rewritten as :
(a – b) x + (a +b) y – (a2 – 2ab – b2) = 0
(a + b) x + (a + b) y – (a2 + b2) = 0
Using formula for cross multiplication method:
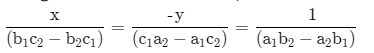
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{x}{(a+b)\times \{-({{a}^{2}}+{{b}^{2}})\}-(a+b)\times \{-({{a}^{2}}-2ab-{{b}^{2}})\}}=\frac{-y}{(a-b)\times \{-({{a}^{2}}+{{b}^{2}})\}-(a+b)\times \{-({{a}^{2}}-2ab-{{b}^{2}})\}}=\frac{1}{(a-b)\times (a+b)-(a+b)\times (a+b)} \)
\(\Rightarrow \frac{x}{-(a+b)({{a}^{2}}+{{b}^{2}})+(a+b)({{a}^{2}}-2ab-{{b}^{2}})}=\frac{-y}{-(a-b)({{a}^{2}}+{{b}^{2}})+(a+b)({{a}^{2}}-2ab-{{b}^{2}})}=\frac{1}{(a-b)(a+b)-{{(a+b)}^{2}}} \)
\(\Rightarrow \frac{x}{(a+b)[-({{a}^{2}}+{{b}^{2}})+(a+b)({{a}^{2}}-2ab-{{b}^{2}})]}=\frac{-y}{(a+b)({{a}^{2}}-2ab-{{b}^{2}})-(a-b)({{a}^{2}}+{{b}^{2}})}=\frac{1}{(a+b)(a-b-a-b)} \)
\(\Rightarrow \frac{x}{(a+b)(-2ab-2{{b}^{2}})}=\frac{-y}{{{a}^{3}}-{{a}^{2}}b-3a{{b}^{2}}-{{b}^{3}}-{{a}^{3}}-a{{b}^{2}}+{{a}^{2}}b+{{b}^{3}}}=\frac{1}{(a+b)(-2b)} \)
\(\Rightarrow \frac{x}{-(a+b)(2a+2b)b}=\frac{-y}{-4a{{b}^{2}}}=\frac{1}{-2b(a+b)} \)
\(\Rightarrow \frac{x}{-2(a+b)(a+b)b}=\frac{1}{-2b(a+b)}\Rightarrow x=a+b \)
\(and\text{ }\frac{-y}{-4a{{b}^{2}}}=\frac{1}{-2b(a+b)}\Rightarrow y=\frac{2ab}{a+b} \)
Hence, the solution of the given system of equations is x = a + b, \(y=\frac{2ab}{a+b} \)
Example 9: Solve the following system of equations by cross-multiplications method.
a(x + y) + b (x – y) = a2 – ab + b2
a(x + y) – b (x – y) = a2 + ab + b2
Sol: The given system of equations can be rewritten as
ax + bx + ay – by – ( a2 – ab + b2) = 0
⇒ (a + b) x + (a – b) y – (a2 – ab + b2) = 0 ….(1)
And ax – bx + ay + by – (a2 + ab + b2) = 0
⇒ (a – b) x + (a + b) y – (a2 + ab + b2) = 0 …(2)
Using formula for cross multiplication method:
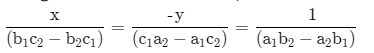
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{x}{(a-b)\times \{-({{a}^{2}}+ab+{{b}^{2}})\}-(a+b)\times \{-({{a}^{2}}-ab+{{b}^{2}})\}}=\frac{-y}{(a+b)\times \{-({{a}^{2}}+ab+{{b}^{2}})\}-(a-b)\times \{-({{a}^{2}}-ab+{{b}^{2}})\}}=\frac{1}{(a+b)\times (a+b)-(a-b)(a-b)} \)
\(\Rightarrow \frac{x}{-(a-b)({{a}^{2}}+ab+{{b}^{2}})+(a+b)({{a}^{2}}-ab+{{b}^{2}})}=\frac{-y}{-(a+b)({{a}^{2}}+ab+{{b}^{2}})+(a-b)({{a}^{2}}-ab+{{b}^{2}})}=\frac{1}{{{(a+b)}^{2}}-{{(a-b)}^{2}}}\)
\(\Rightarrow \frac{x}{-({{a}^{3}}-{{b}^{3}})+({{a}^{3}}+{{b}^{2}})}=\frac{-y}{-{{a}^{3}}-2{{a}^{2}}b-2a{{b}^{2}}-{{b}^{3}}+{{a}^{3}}-2{{a}^{2}}b+2a{{b}^{2}}-{{b}^{3}}}=\frac{1}{{{a}^{2}}+2ab+{{b}^{2}}-{{a}^{2}}+2ab-{{b}^{2}}}\)
\(\Rightarrow \frac{x}{2{{b}^{3}}}=\frac{-y}{-4{{a}^{2}}b-2{{b}^{3}}}=\frac{1}{4ab} \)
\(\Rightarrow \frac{x}{2{{b}^{3}}}=\frac{-y}{-2b(2{{a}^{2}}+{{b}^{2}})}=\frac{1}{4ab}\)
\(\Rightarrow \frac{x}{2{{b}^{3}}}=\frac{1}{4ab}\Rightarrow x=\frac{{{b}^{2}}}{2a}\)
\(and\text{ }\frac{-y}{-2b(2{{a}^{2}}+{{b}^{2}})}=\frac{1}{4ab}\Rightarrow y=\frac{2{{a}^{2}}+{{b}^{2}}}{2a}\)
Hence, the solution is \(x=\frac{{{b}^{2}}}{2a},y=\frac{2{{a}^{2}}+{{b}^{2}}}{2a}\)
Example 10: Solve the following system of equations by the method of cross-multiplication.
\(\frac{a}{x}-\frac{b}{y}=0;\text{ }\frac{a{{b}^{2}}}{x}+\frac{{{a}^{2}}b}{y}={{a}^{2}}+{{b}^{2}};\)
Where x ≠ 0, y ≠ 0
Sol: The given system of equations is
\(\frac{a}{x}-\frac{b}{y}=0\) ………(1)
\(\frac{a{{b}^{2}}}{x}+\frac{{{a}^{2}}b}{y}-\left( {{a}^{2}}+{{b}^{2}} \right)=0\) ………(2)
Putting \(\frac { a }{ x }=u\) and \(\frac { b }{ y }=v\) in equatinos (1) and (2) the system of equations reduces to
u – v + 0 = 0
b2u + a2v – (a2 + b2) = 0
Using formula for cross multiplication method:
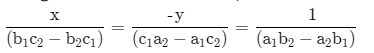
So, from equation (1) and (2) we can write the value of a,b and c.
\(\Rightarrow \frac{u}{{{a}^{2}}+{{b}^{2}}-{{a}^{2}}\times 0}=\frac{-v}{-({{a}^{2}}+{{b}^{2}})-{{b}^{2}}\times 0}=\frac{1}{{{a}^{2}}-(-{{b}^{2}})}\)
\(\Rightarrow \frac{u}{{{a}^{2}}+{{b}^{2}}}=\frac{-v}{-({{a}^{2}}+{{b}^{2}})}=\frac{1}{{{a}^{2}}+{{b}^{2}}} \)
\(\Rightarrow \frac{u}{{{a}^{2}}+{{b}^{2}}}=\frac{1}{{{a}^{2}}+{{b}^{2}}}\Rightarrow u=1 \)
\(and\text{ }\frac{-v}{-({{a}^{2}}+{{b}^{2}})}=\frac{1}{{{a}^{2}}+{{b}^{2}}}\Rightarrow v=1 and\text{ u}=\frac{a}{x}=1\Rightarrow x=a \)
\(v=\frac{b}{y}=1\Rightarrow y=b \)
Hence, the solution of the given system of equations is x = a, y = b.