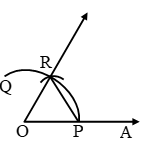
Construction Of An Angle Using Compass And Ruler To draw an angle equal to a given angle In this section, we will learn how to construct angles of 60º, 30º, 90º, 45º and 120º with the help of ruler and compasses only. Construction Of Some Standard Angles Construction of an Angle of 60º In order to construct an angle of 60º with the help of ruler and compasses only, we … [Read more...] about How Do You Construct An Angle With Compass And Ruler