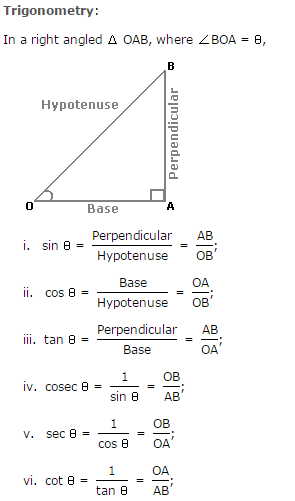
Heights And Distances

Angle Of Elevation
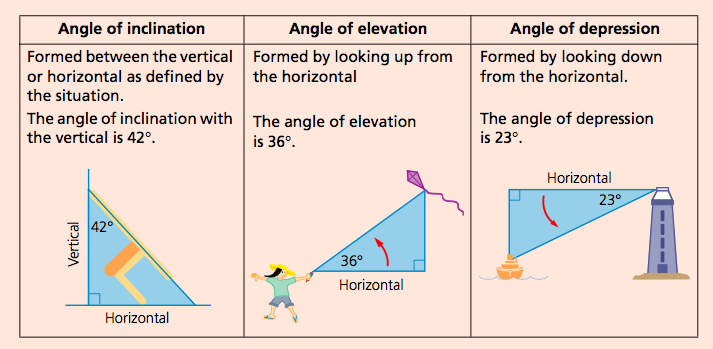
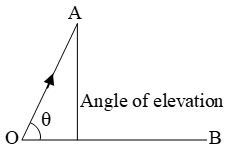
The angle of elevation of the point viewed is the angle formed by the line of sight with the horizontal when the point being viewed is above the horizontal level, i.e. the case when we raise our head to look at the object. (see fig.)
Angle Of Depression
The angle of depression of a point on the object being viewed is the angle formed by the line of sight with the horizontal when the point is below the horizontal level, i.e. the case when we lower our head to look at the point being viewed. (See fig.)

More on RS Aggarwal Class 10 Height and Distance Solutions
Heights And Distances With Examples
Example 1: The shadow of a building is 20 m long when the angle of elevation of the sun is 60º. Find the height of the building.
Sol. Let AB be the building and AC be its shadow.
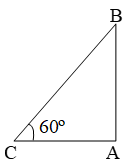
Then, AC = 20 m and ∠ACB = 60º.
Let AB = h.
Then, \(\frac { AB }{ AC }\) = tan 60º = √3
⇒ h/20 = √3
∴ h = (20 × √3 )m = (20 × 1.732) m
= 34.64 m.
Example 2: If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
Sol. Let AB be the vertical pole and AC be its shadow.

Let the angle of elevation be θ. Then,
AB = 6 m, AC = 2 √3 m
and ∠ACB = θ.
\(\text{Now, tan }\theta =\frac{AB}{AC}=\frac{6}{2\sqrt{3}}=\sqrt{3}=\text{ tan }60{}^\text{o}.\)
∴ θ = 60º.
Example 3: A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder.
Sol. Let AB be the wall and CB, the ladder.
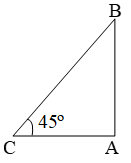
Then, AC = 3m and ∠ACB = 45º
\(\text{Now, }\frac{CB}{AC}=\sec \text{ 45}{}^\text{o}=\sqrt{2}\Rightarrow \frac{CB}{3}=\sqrt{2} \)
∴ Length of the ladder = CB = 3 √2
= (3 × 1.41) m = 4.23 m
Example 4: A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable.
Sol. Let B be the balloon and AB be the vertical height. Let C be the meteorological station and CB be the cable.
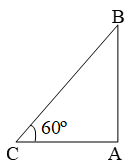
Then, BC = 200 m and ∠ACB = 60º
\( \text{Then, }\frac{AB}{BC}=\text{sin }60{}^\text{o}=\frac{\sqrt{3}}{2} \)
\( \Rightarrow \frac{AB}{200}=\frac{\sqrt{3}}{2} \)
\( \Rightarrow AB=\left( \frac{200\times \sqrt{3}}{2} \right)m=173.2\text{ }m. \)
Example 5: The pilot of a helicopter, at an altitude of 1200m finds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships.
Sol. Let B the position of the helicopter and let C, D be the ships. Let AB be the vertical height.
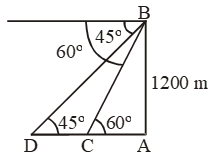
Then, AB = 1200 m,
∠ACB = 60º and ∠ADB = 45º.
\( \text{Then, }\!\!~\!\!\text{ }\frac{AD}{AB}=\text{cot 45 }\!\!{}^\text{o}\!\!\text{ = 1} \)
\( \Rightarrow \frac{AD}{1200}=1\Rightarrow \text{AD = 1200 m} \)
\( \text{And, }\!\!~\!\!\text{ }\frac{AC}{AB}=\text{cot 60 }\!\!{}^\text{o}\!\!\text{ }=\frac{1}{\sqrt{3}}\text{ } \)
\( \Rightarrow \frac{AC}{1200}=\frac{1}{\sqrt{3}}\text{ } \)
\( \Rightarrow AC=\frac{1200}{\sqrt{3}}=400\sqrt{3}\text{ m}\text{.} \)
Example 6: A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
Sol. Let AB be the tower and BC be the flagstaff.
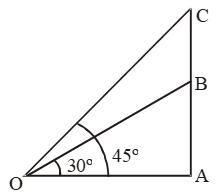
Then, BC = 7 m. Let AB = h.
Let O be the point of observation.
Then, ∠AOB = 30º and ∠AOC = 45º.
\( \text{Now, }\frac{OA}{AC}=\text{cot 45 }\!\!{}^\text{o}\!\!\text{ }=1 \)
⇒ OA = AC = h + 7.
\( \text{And, }\frac{OA}{AB}=\text{cot }30{}^\text{o}=\sqrt{3} \)
\( \Rightarrow \frac{OA}{h}=\sqrt{3}\Rightarrow OA=h\sqrt{3} \)
∴ h + 7 = h√3
\( \Rightarrow \frac{7}{\sqrt{3}-1}\times \frac{\sqrt{3}+1}{\sqrt{3}+1}=\frac{7(\sqrt{3}+1)}{2}=9.562\text{ }m \)
Example 7: From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower.
Sol. Let AB be the building and CD be the tower.
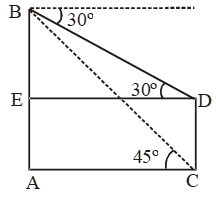
Then, AB = 30 m. Let DC = x.
Draw DE ⊥ AB. Then AE = CD = x.
∴ BE = (30 – x) m.
\( \text{Now, }\frac{AC}{AB}=\text{cot 45 }\!\!{}^\text{o}\!\!\text{ }=1 \)
\( \Rightarrow \frac{AC}{30}=1\Rightarrow AC=30\text{ }m \)
∴ DE = AC = 30 m.
\( \frac{BE}{DE}=\text{tan }30{}^\text{o}=\frac{1}{\sqrt{3}}\Rightarrow \frac{BE}{30}=\frac{1}{\sqrt{3}} \)
\( \Rightarrow BE=\frac{30}{\sqrt{3}} \)
\( CD=AE=AB-BE=\left( 30-\frac{30}{\sqrt{3}} \right) \)
\( =30\left( 1-\frac{1}{\sqrt{3}} \right)\,m \)
Example 8: From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower.
Sol. Let AB be the cliff and CD be the tower.
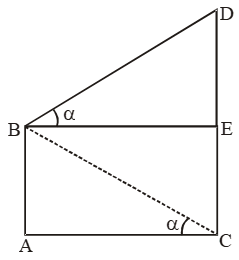
Then, AB = 25 m. From B draw BE ⊥ CD.
Let ∠EBD = ∠ACB = α.
\( \text{Now, }\frac{\text{DE}}{\text{BE}}=\text{tan }\alpha \text{ and }\frac{\text{AB}}{\text{AC}}=\text{tan }\alpha \text{ } \)
\( \frac{DE}{BE}=\frac{AB}{AC}\text{ }So,\text{ }DE=AB \) [ ∵ BE = AC]
∴ CD = CE + DE = AB + AB = 2AB = 50m
Example 9: The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
Sol. Let AB be the pole and AC be its shadow.
Then, θ = 60º and AC = 30 m.
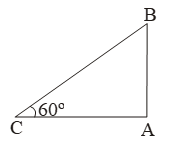
\( \frac{AB}{AC}=\text{tan }60{}^\text{o} \)
\( \Rightarrow \frac{AB}{30}=\sqrt{3}\Rightarrow AB=30\sqrt{3}\,\,m \)
Example 10: When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high.
Sol. Let AB be the building and AC be its shadow.
Then, AB = 50 m and θ = 30º.
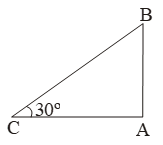
\( \frac{AC}{AB}=\text{cot 3}0{}^\text{o}=\sqrt{3} \)
\( \Rightarrow \frac{AC}{50}=\sqrt{3} \)
⇒ AC = 50√3 cm.
Example 11: If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions.
Sol. When AB = 15m, θ = 30º,
\( \text{then }\frac{AC}{AB}=\text{tan}30{}^\text{o} \)
\( \Rightarrow AC=\frac{15}{\sqrt{3}}m. \)
When AB = 15m, θ = 60º,
\( \text{then }\frac{AC}{AB}=\text{tan6}0{}^\text{o} \)
⇒ AC = 15√3 m.
∴ Diff. in lengths of shadows
\( =\left( 15\sqrt{3}-\frac{15}{\sqrt{3}} \right) \)
\( =\frac{30}{\sqrt{3}}=10\sqrt{3}\,\,m \)
Example 12: The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the poles.
Sol. Let AB and CD be the poles such that
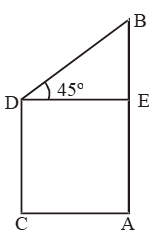
AB = 80 m and CD = 62.5 m.
Draw DE ⊥ AB. Then, ∠EDB = 45º
Now, BE = AB – AE = AB – CD = 17.5
\(\frac{DE}{BE}=\text{cot }45{}^\text{o}=1\)
⇒ DE = BE = 17.5 m.
Example 13: If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake.
Sol. Let C be the cloud and C’ be its reflection in the lake.
Let CS = C’S = x.
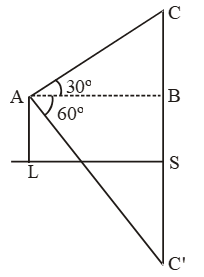
\( \text{Now, }\frac{BC}{AB}=\text{tan }30{}^\text{o}=\frac{1}{\sqrt{3}} \)
\( \Rightarrow x-200=\frac{AB}{\sqrt{3}} \)
\( \text{Also, }\frac{BC’}{AB}=\text{tan }60{}^\text{o}=\sqrt{3} \)
\( \Rightarrow ~~x+200=(AB)\sqrt{3}. \)
\( \sqrt{3}(x-200)=\frac{x+200}{\sqrt{3}}\text{ or }x=\text{400}. \)
∴ CS = 400 m.
Example 14: A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level.
Sol. Let C be the centre of the balloon and O be the position of the observer at the horizontal line OX. Let OA and OB be the tangents to the balloon so that ∠AOB = α, ∠XOC = β and
CA = CB = γ.
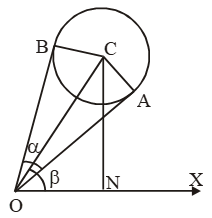
Clearly, right angled triangles OAC and OBC are congruent.
∠AOC = ∠BOC = α/2.
Let CN ⊥ OX.
\( \text{Now, }\frac{OC}{CA}=\text{cosec }\!\!~\!\!\text{ }\frac{\alpha }{2} \)
\( \Rightarrow OC=\gamma \text{ cosec }\!\!~\!\!\text{ }\frac{\alpha }{2}\text{ }…\text{(i)} \)
\( \text{Also, }\frac{CN}{OC}=\sin \beta \)
\( \Rightarrow CN=OC\text{ sin }\beta =\gamma \text{ cosec }\!\!~\!\!\text{ }\frac{\alpha }{2}\sin \beta \text{ }\left[ \text{Using}\left( \text{i} \right) \right] \)
Example 15: The banks of a river are parallel. A swimmer starts from a point on one of the banks and swims in a straight line inclined to the bank at 45º and reaches the opposite bank at a point 20 m from the point opposite to the starting point. Find the breadth of the river.
Sol. Let A be the starting point and B, the end point of the swimmer. Then AB = 20 m and ∠BAC = 45º.

\( \text{Now, }\frac{BC}{AB}=\text{sin}45{}^\text{o}=\frac{1}{\sqrt{2}} \)
\( \Rightarrow \frac{BC}{20}=\frac{1}{\sqrt{2}} \)
\( \Rightarrow BC=\frac{20\times \sqrt{2}}{2}=14.14\text{ }m. \)
Example 16: A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore.
Sol. Let AB be the cliff and C and D be the two positions of the fishing trawler.
Then, ∠ACB = 30º and ∠ADB = 60º
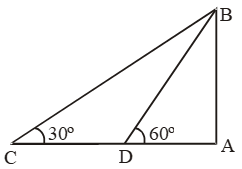
Let AB = h.
\( \text{Now, }\frac{AD}{AB}=\text{cot }60{}^\text{o}=~\frac{1}{\sqrt{3}} \)
\( \Rightarrow AD=\frac{h}{\sqrt{3}} \)
\( \text{And, }\frac{AC}{AB}=\text{cot 3}0{}^\text{o}=~\sqrt{3} \)
⇒ AC = √3 h
\( CD=ACAD=\left( \sqrt{3}\,h-\frac{h}{\sqrt{3}} \right)=\frac{2h}{\sqrt{3}} \)
Let u m/min be the uniform speed of the trawler.
Distance covered in 6 min = 6u metres.
\( CD=6u~\Rightarrow \frac{2h}{\sqrt{3}}=6u\Rightarrow h=3\sqrt{3}\,\,u \)
\( Now,\text{ }AD=\frac{h}{\sqrt{3}}=\frac{3\sqrt{3}\,\,u}{\sqrt{3}}=3u \)
Time taken by trawler to reach A
\( =\frac{dis\tan ce\,AD}{speed}\Rightarrow A=\frac{3u}{u}=3\min \)
Example 17: A boat is being rowed away from a cliff 150m high. At the top of the cliff the angle of depression of the boat changes from 60º to 45º in 2 minutes. Find the speed of the boat.
Sol. Let AB be the cliff and C and D be the two positions of the ship. Then, AB = 150 m,
∠ACB = 60º and ∠ADB = 45º.
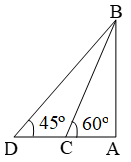
\( Now,\frac{AD}{AB}=\text{cot }45{}^\text{o}=1 \)
\( \Rightarrow \frac{AD}{150}=1\Rightarrow AD\text{ }=\text{ }150\text{ }m. \)
\( \frac{AC}{AB}=\text{cot 60}{}^\text{o}=\frac{1}{\sqrt{3}}\Rightarrow \frac{AC}{150}=\frac{1}{\sqrt{3}} \)
\( \Rightarrow AC=\frac{150}{\sqrt{3}}=50\sqrt{3}=\text{ }86.6\text{ }m \)
∴ CD = AD – AC = (150 – 86.6) m = 63.4 m
Thus, distance covered in 2 min. = 63.4 m
∴ Speed of the boat
\( =\left( \frac{63.4}{2}\times \frac{60}{1000} \right)\,\,km/hr.=\text{ }1.9\text{ }km/hr. \)
Example 18: A tower is 100√3 metres high. Find the angle of elevation of its top from a point 100 metres away from its foot.
Sol. Let AB be the tower of height 100√3 metres, and let C be a point at a distance of 100 metres from the foot of the tower.
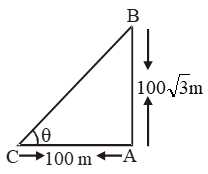
Let θ be the angle of elevation of the top of the tower from point C.
In ∆CAB, we have
\( \tan \theta =\frac{AB}{AC} \\ \)
\( \Rightarrow \tan \theta =\frac{100\sqrt{3}}{100}=\sqrt{3} \)
⇒ θ = 60º
Hence, the angle of elevation of the top of the tower from a point 100 metres away from its foot is 60º.
Example 19: From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
Sol. Let BC be the tower of height h metre and CD be the water tank of height h1 metre.
Let A be a point on the ground at a distance of 40 m away from the foot B of the tower.

In ∆ABD, we have tan 45º = \(\frac { BD }{ AB }\)
\( \Rightarrow 1=\frac{h+{{h}_{1}}}{40}\Rightarrow ~~h+{{h}_{1}}=40\text{ }m~\text{ }\text{……}\left( \text{i} \right) \)
In ∆ABC, we have
\( \text{tan }30{}^\text{o}\text{ }=\frac{BC}{AB}\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{40} \)
\( \Rightarrow h=\frac{40}{\sqrt{3}}=\frac{40\sqrt{3}}{3}=23.1\text{ m} \)
Substituting the value of h in (i), we get
23.1 + h1 = 40
⇒ h1 = (40 – 23.1)m = 16.9 m
Example 20: Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by
\(\text{cot }\theta =\frac{b\,\,\cot \,\,\alpha -a\,\,\cot \,\,\beta }{b-a} \)
Sol. Let AB be the leaning tower and let C and D be two given stations at distances a and b respectively from the foot A of the tower.
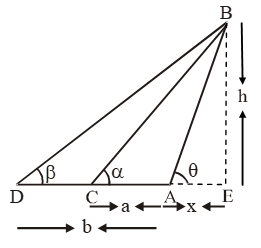
Let AE = x and BE = h
In ∆ABE, we have
\( \tan \theta =\frac{BE}{AE}\Rightarrow \tan \theta =\frac{h}{x} \)
⇒ x = h cot θ ….(i)
In ∆CBE, we have
\( \tan \alpha =\frac{BE}{CE} \)
\( \Rightarrow \tan \alpha =\frac{h}{a+x} \)
⇒ a + x = h cot α
⇒ x = h cot α – a ….(ii)
In ∆DBE, we have
\( \tan \beta =\frac{BE}{DE} \)
\( \Rightarrow \tan \beta =\frac{h}{b+x} \)
⇒ b + x = h cot β
⇒ x = h cot β– b ….(iii)
From equations (i) and (ii), we have
h cot θ= h cot α– a
⇒ h (cot α– cot θ) = a
\( \Rightarrow h=\frac{a}{\cot \alpha -\cot \theta } \)
From equation (i) and (iii), we get
h cot θ= h cot β– b
⇒ h (cot β– cot θ) = b
\( \Rightarrow h=\frac{b}{\cot \beta -\cot \theta } \)
Equating the values of h from equations (iv) and (v), we get
\( \frac{a}{\cot \alpha -\cot \theta }=\frac{b}{\cot \beta -\cot \theta } \)
⇒ a(cot β– cot θ) = b(cot α– cot θ)
⇒ (b – a) cot θ= b cot α– a cot β
\( \cot \theta =\frac{b\,\,\cot \alpha -a\cot \beta }{b-a} \)
Example 21: If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is \(\frac{h(\tan \alpha +\tan \beta \,)}{\tan \beta -\tan \alpha } \).
Sol. Let AB be the surface of the lake and let P be a point of observation such that AP = h metres. Let C be the position of the cloud and C´ be its reflection in the lake. Then, CB = C´B. Let PM be perpendicular from P on CB. Then,
∠CPM = α and ∠MPC´= β Let CM = x.
Then, CB = CM + MB = CM + PA = x + h.
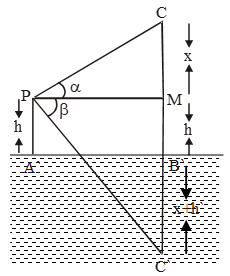
In ∆CPM, we have
\( \tan \alpha =\frac{CM}{PM} \)
\( \Rightarrow \tan \alpha =\frac{x}{AB} \)
⇒ AB = x cot α ….(i)
In ∆PMC´, we have
\( \tan \beta =\frac{C\acute{\ }M}{PM} \)
\( \Rightarrow \tan \beta =\frac{x+2h}{AB} \)
[∵ C´M = C´B + BM = x + h + h]
⇒ AB = (x + 2h) cot β ….(ii)
From (i) and (ii), we have
x cot α= (x + 2h) cot β
⇒ x(cot α– cot β) = 2h cot β
\( \Rightarrow x\left( \frac{1}{\tan \alpha }-\frac{1}{\tan \beta } \right)=\frac{2h}{\tan \beta } \)
\( \Rightarrow x\left( \frac{\tan \beta -\tan \alpha }{\tan \alpha \tan \beta } \right)=\frac{2h}{\tan \beta } \)
\( \Rightarrow x=\frac{2h\tan \alpha }{\tan \beta -\tan \alpha } \)
Hence,
Height of the cloud = x + h
\( =\frac{2h\tan \alpha }{\tan \beta -\tan \alpha }+h \)
\( =\frac{2h\tan \alpha +h\tan \beta -h\tan \alpha }{\tan \beta -\tan \alpha } \)
\( =\frac{h(\tan \alpha +\tan \beta \,)}{\tan \beta -\tan \alpha } \)
Example 22: There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree.
Sol. Let OA be the tree of height h metre.
In triangles POA and QOA, we have
\( \text{tan }30{}^\text{o}=\frac{OA}{OP}\text{ and tan }45{}^\text{o}=\frac{OA}{OQ} \)
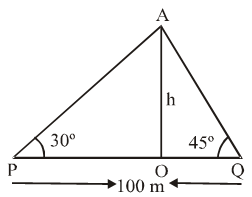
\( \Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{OP}\text{ and }1=\frac{h}{OQ} \)
⇒ OP = √3 h and OQ = h
⇒ OP + OQ = √3 h + h ⇒ PQ = (√3+ 1)h
⇒ 100 = (√3 + 1)h [∵ PQ = 100 m]
\( \Rightarrow h=\frac{100}{\sqrt{3}+1}\Rightarrow h=\frac{100(\sqrt{3}-1)}{2}\text{ m} \)
⇒ h = 50(1.732 – 1) m = 36.6 m
Hence, the height of the tree is 36.6 m
Example 23: The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
Sol. Let AB be the cliff and O be the fixed point such that the angle of elevation of the cliff from O is θ i.e. ∠AOB = θ. Let ∠AOC = φ and
OC = k metres. From C draw CD and CE perpendiculars on AB and OA respectively.
Then, ∠DCB = α.
Let h be the height of the cliff AB.
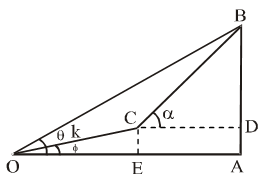
In ∆OCE, we have
\( \sin \phi =\frac{CE}{OC} \)
\( \Rightarrow \sin \phi =\frac{CE}{k} \)
⇒ CE = k sin φ …(i) [∵ CE = AD]
⇒ AD = k sin φ
\( \text{And, cos}\phi =\frac{OE}{OC} \)
\( \Rightarrow \text{cos}\phi =\frac{OE}{k} \)
⇒ OE = k cos φ ….(ii)
In ∆ OAB, we have
\( \text{tan }\theta =\frac{AB}{OA} \)
\( \Rightarrow \text{tan }\theta =\frac{h}{OA} \)
⇒ OA = h cot θ ….(iii)
CD = EA = OA – OE
= h cot θ – k cos φ …..(iv) [Using eqs.(ii) and (iii)]
and, BD = AB – AD = AB – CE
= (h – k sin φ) ….(v) [Using equation (i)]
In ∆BCD, we have
\( \text{tan}\alpha =\frac{BD}{CD}\Rightarrow \text{ tan}\alpha =\frac{h-k\sin \varphi }{h\cot \theta -k\cos \varphi } \) [Using equations (iv) and (v)]
\( \Rightarrow \frac{1}{\cot \alpha }=\frac{h-k\sin \varphi }{h\cot \theta -k\cos \varphi} \)
⇒ h cot α – k sin φ cot α = h cot θ – k cos φ
⇒ h(cot θ – cot α) = k(cos φ – sin φcot α)
\( \Rightarrow h=\frac{k(\cos \varphi -\sin \varphi \cot \alpha )}{\cot \theta -\cot \alpha } \)
Example 24: At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
Sol. Let F be the foot and S be the summit of the mountain FOS. Then, ∠OFS = 45º and therefore ∠OSF = 45º. Consequently,
OF = OS = h km(say).
Let FP = 1000 m = 1 km be the slope so that
∠OFP = 30º. Draw PM ⊥OS and PL ⊥OF.
Join PS. It is given that ∠MPS = 60º.
In ∆FPL, We have
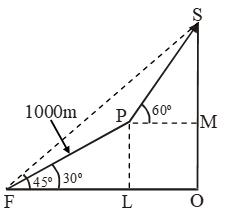
\( \text{sin }30{}^\text{o}=\frac{PL}{PF} \)
\( \Rightarrow PL=PF\text{ sin }30{}^\text{o}=\left( 1\times \frac{1}{2} \right)=\frac{1}{2}km. \)
\( OM=PL=\frac{1}{2}km \)
\( \Rightarrow MS=OS-OM=~\left( h-\frac{1}{2} \right)km~~~~\ldots .\left( i \right) \)
\( \text{Also, cos }30{}^\text{o}=\frac{FL}{PF} \)
\( \Rightarrow FL=PF\text{ cos }30{}^\text{o}=\left( 1\times \frac{\sqrt{3}}{2} \right)=\frac{\sqrt{3}}{2}km \)
Now, h = OS = OF = OL + LF
\( \Rightarrow h=OL+\frac{\sqrt{3}}{2} \)
\( \Rightarrow OL=\left( h-\frac{\sqrt{3}}{2} \right)km \)
\( \Rightarrow PM=\left( h-\frac{\sqrt{3}}{2} \right)km \)
In ∆PSM, we have
\( \text{tan }60{}^\text{o}=\frac{SM}{PM} \)
⇒ SM = PM. tan 60º …..(ii)
\( \Rightarrow \left( h-\frac{1}{2} \right)=\left( h-\frac{\sqrt{3}}{2} \right)\sqrt{3} \) [Using equations (i) and (ii)]
\( \Rightarrow h-\frac{1}{2}=h\sqrt{3}-\frac{3}{2} \)
⇒ h(√3 – 1) = 1
\( \Rightarrow h=\frac{1}{\sqrt{3}-1} \)
\( \Rightarrow h=\frac{\sqrt{3}+1}{(\sqrt{3}-1)\,(\sqrt{3}+1)}=\frac{\sqrt{3}+1}{2} \)
\( =\frac{2.732}{2}=1.336\text{ }km \)
Hence, the height of the mountain is 1.366 km.
Example 25: The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is \(\frac{d}{\sqrt{{{\cot }^{2}}\alpha +{{\cot }^{2}}\beta }} \)
Sol. Let OP be the tower and let A and B be two points due south and east respectively of the tower such that ∠OAP = αand ∠OBP = β.
Let OP = h. In ∆OAP, we have
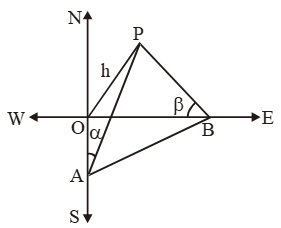
\( \tan \alpha =\frac{h}{OA} \)
⇒ OA = h cot α ….(i)
In ∆OBP, we have
\( \tan \beta =\frac{h}{OB} \)
⇒ OB = h cot β. ….(ii)
Since OAB is a right angled triangle. Therefore,
AB2 = OA2 + OB2
⇒ d2 = h2 cot2 α + h2 cot2 β
\( \Rightarrow h=\frac{d}{\sqrt{{{\cot }^{2}}\alpha +{{\cot }^{2}}\beta }} \) [Using (i) and (ii)]
Example 26: The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is \(\frac{AB\sin \alpha \sin \beta }{\sqrt{{{\sin }^{2}}\alpha -{{\sin }^{2}}\beta }} \)
Sol. Let OP be the tower and let A be a point due north of the tower OP and let B be the point due west of A. Such that ∠OAP = and ∠OBP = Let h be the height of the tower.
In right angled triangles OAP and OBP, we have
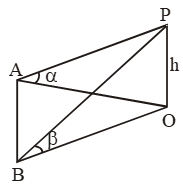
\( \tan \alpha =\frac{h}{OA}\text{ and }\tan \beta =\frac{h}{OB} \)
⇒ OA = h cot α and OB = h cot β.
In ∆OAB, we have
OB2 = OA2 + AB2
⇒ AB2 = OB2 – OA2
⇒ AB2 = h2 cot2 β– h2 cot2 α
⇒ AB2 = h2 [cot2 β– cot2 α]
⇒ AB2 = h2[(cosec2 β– 1) – (cosec2 α– 1)]
⇒ AB2 = h2(cosec2 β– cosec2 α)
\( \Rightarrow A{{B}^{2}}={{h}^{2}}\left( \frac{{{\sin }^{2}}\alpha -{{\sin }^{2}}\beta }{{{\sin }^{2}}\alpha {{\sin }^{2}}\beta } \right) \)
\( \Rightarrow h=\frac{AB\sin \alpha \sin \beta }{\sqrt{{{\sin }^{2}}\alpha -{{\sin }^{2}}\beta }} \)
Example 27: An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant.
Sol. Let P and Q be the positions of two aeroplanes when Q is vertically below P and OP = 4000 m. Let the angles of elevation of P and Q at a point A on the ground be 60º and 45º respectively.
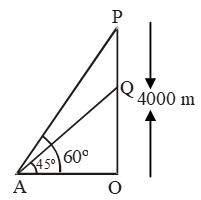
\( \text{tan }60{}^\text{o}=\frac{OP}{OA}\text{ and tan 45}{}^\text{o}=\frac{OQ}{OA} \)
\( \Rightarrow \sqrt{3}=\frac{4000}{OA}\text{ and 1=}\frac{OQ}{OA} \)
\( \Rightarrow OA=\frac{4000}{\sqrt{3}}\text{ and }OQ=OA \)
\( \Rightarrow OQ=\frac{4000}{\sqrt{3}}m \)
In triangles AOP and AOQ, we have
∴ Vertical distance between the aeroplanes
= PQ = OP – OQ
\(=\left( 4000-\frac{4000}{\sqrt{3}} \right)=4000\frac{(\sqrt{3}-1)}{\sqrt{3}}m \)
= 1690.53 m