Division Of A Line Segment Into A Given Ratio

Division Of A Line Segment Into A Given Ratio

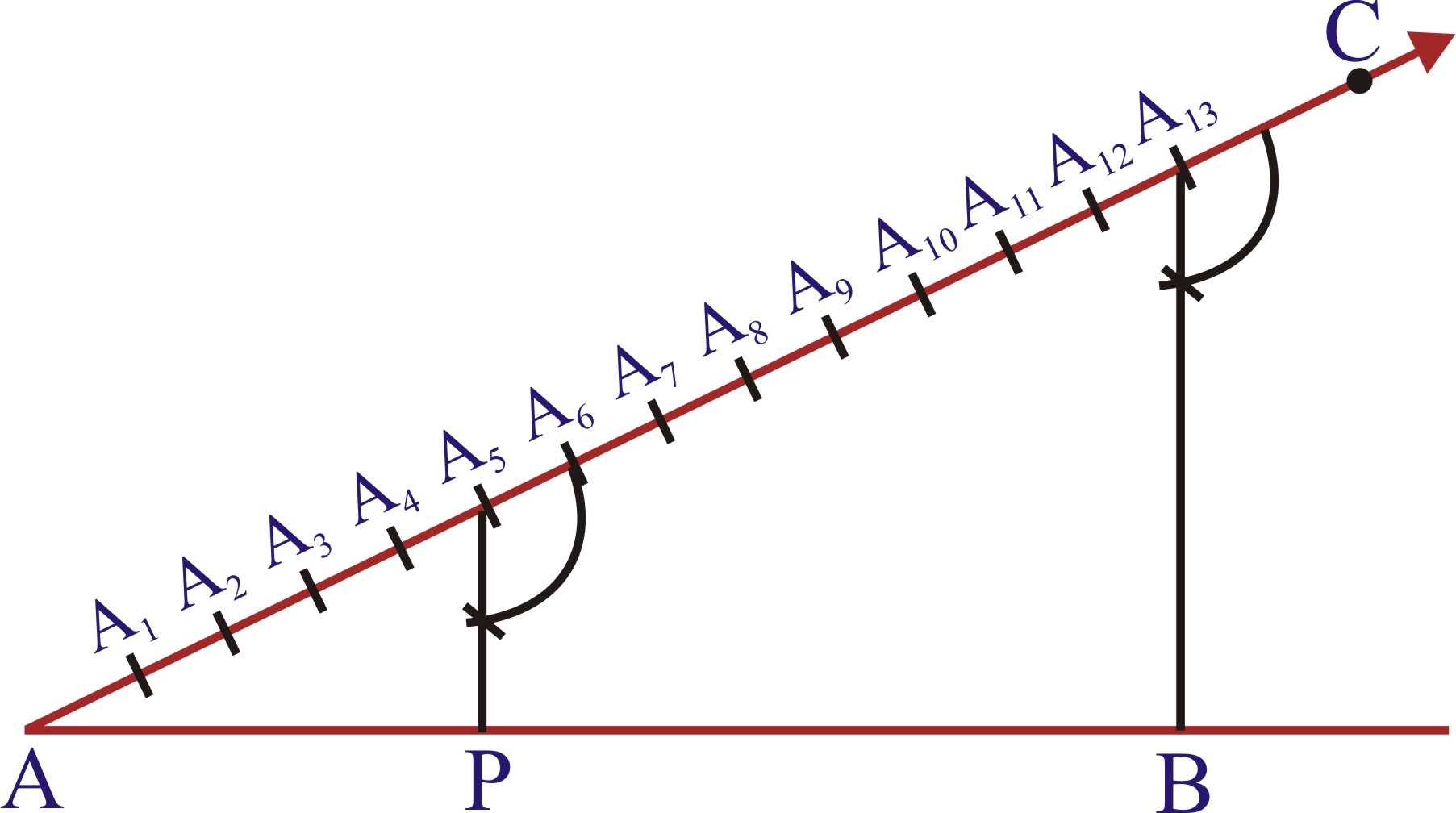
Given a line segment AB, we want to divide it in the ratio m : n, where both m and n are positive integers. To help you to understand it, we shall take m = 3 and n = 2.
Steps of Construction:
1.  Draw any ray AX, making an acute angle with AB.
2.  Locate 5(= m + n) points A₁, A₂,  A₃, A₄ and A₅ on AX so that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.
3.  Join BA₅.
4.  Through the point A₃ (m = 3), draw a line parallel to A₅B (by making an angle equal to ∠AA₅B) at A₃ intersecting AB at the point C (see figure). Then, AC : CB = 3 : 2.

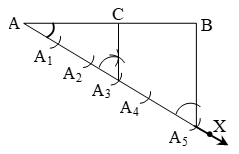
Let use see how this method gives us the required division.
Since A₃C is parallel to A₅B, therefore,
\( \frac{A{{A}_{3}}}{{{A}_{3}}{{A}_{5}}}=\frac{AC}{CB}\text{ }\left( \text{By the Basic Proportionality Theorem} \right) \)
\( \frac{A{{A}_{3}}}{{{A}_{3}}{{A}_{5}}}=\frac{3}{2}\text{ (By construction) } \)
\( \text{ }\frac{AC}{CB}=\frac{3}{2}\text{ } \)
This shows that C divides AB in the ratio 3 : 2.

Alternative Method
Steps of Construction :
1.  Draw any ray AX making an acute angle with AB.
2.  Draw a ray BY parallel to AX by making ∠ABY equal to ∠BAX.
3.  Locate the points A₁, A₂, A₃ (m = 3) on AX and B₁, B₂ (n = 2) on BY such that AA₁ = A₁A₂ = A₂A₃ = BB₁ = B₁B₂.
4.  Join A₃B₂.

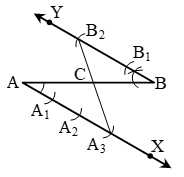
Let it in intersect AB at a point C (see figure)
Then AC : CB = 3 : 2
Whey does this method work ? Let us see.
Here DAA₃C is similar to DAB₂C. (Why ?)
\( \text{Then }\frac{A{{A}_{3}}}{B{{B}_{2}}}=\frac{AC}{BC}\)
\( \frac{A{{A}_{3}}}{B{{B}_{2}}}=\frac{3}{2}\text{ (By construction) } \)
\( \text{ }\frac{AC}{BC}=\frac{3}{2} \)
In fact, the methods given above work for dividing the line segment in any ratio.
We now use the idea of the construction above for constructing a triangle similar to a given triangle whose sides are in a given ratio with the corresponding sides of the given triangle.