Distance Between Two Points
Distance Between Two Points Formula

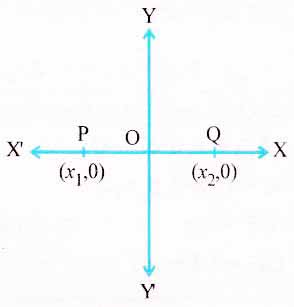
(1) Distance between two points on X-axis :
The coordinate axes in the coordinate plane can be treated as number lines.
If P(x1, 0) and Q(x2, 0) are two points on X-axis, the distance between them is taken as
PQ = |x1-x2| ……….(i)
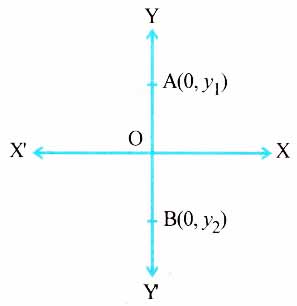
(2) Distance between two points on Y-axis:
If the points A(0, y1) and B(0, y2) are two points on Y-axis, the distance between them is taken as
AB = |y1-y2| ……….(ii)
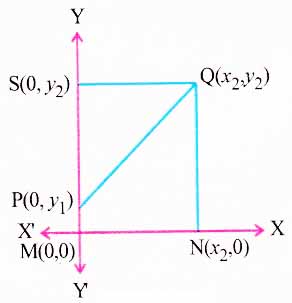
(3) Distance between P(x1, y1) and Q(x2, y2):
Let P(x1, y1) and Q(x2, y2) be two given points in the coordinate plane.
Let M and N be the feet of perpendiculars from P(x1, y1) and Q(x2, y2) respectively to X-axis.
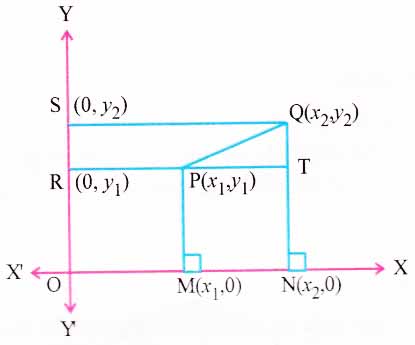
∴ M and N are respectively (x1, 0) and (x2, 0).
MN = |x1-x2| ……….(i)
Let R and S be the feet of perpendiculars from P(x1, y1) and Q(x2, y2) to Y-axis.
R and S are respectively (0, y1) and (0, y2).
RS = |y1-y2| ……….(ii)
Let PR and QN intersect in T.
Clearly in ∆PQT, ∠PTQ is a right angle.
Using Pythagoras’ theorem we have,
PQ2 = PT2 + QT2 = MN2 + RS2
because QTRS and PTNM are rectangles.
Now, by (i) and (ii), we have
PQ2 = MN2 + RS2
=|x1-x2|2 + |y1-y2|2
= (x1-x2)2 + (y1-y2)2
∴ \( PQ=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}} \)
Formula (iii) gives the distance between two points whose coordinates are (x1, y1) and (x2, y2). The distance between the points P and Q is also denoted by d(P, Q).
Thus, d(P, Q) = PQ
= d(P(x1, y1), Q(x2, y2)) = \(\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}} \)
If P and Q lie on X-axis then also formula remains same.
Here, M = P and N = O.
R = O and S = Q.
MN = OP = |x1-0| = |x1| = |x1-y1| (y1 = 0)
RS = OQ = |0-y2| = |x2-y2| (x2 = 0)
∴ \(PQ=\sqrt { { \left| { { x }_{ 1 } }-{ { x }_{ 2 } } \right| }^{ 2 }+{ \left| { { y }_{ 1 } }-{ { y }_{ 2 } } \right| }^{ 2 } } =\sqrt { { { \left( { { x }_{ 1 } }-{ { x }_{ 2 } } \right) }^{ 2 } }+{ { \left( { { y }_{ 1 } }-{ { y }_{ 2 } } \right) }^{ 2 } } }\)
[Note : P may lie on Y-axis
Here x1 = 0.
Here also PS = |y1-y2| (P = R)
MN = = |0-x2| = |x2-y2|
Similarly if P lies on X-axis, the formula remains same.]
If PQ is parallel to any axis then x1 = x2 or y1 = y2 and formula remains same.
‘Distance’ is also known as a ‘Metric’. Metric plays an important role in all kinds of geometry, including Euclidean geometry. In fact the nature of Metric defines the type of geometry. The following properties of Metric are not only interesting but also very useful.
(1) d(A, B) = AB ≥ 0 i.e. the distance between two points is a non-negative real number.
(2) d(A, B) = AB = 0, if and only if A = B.
(3) d(A, B) = d(B, A) i.e. AB = BA.
(4) If A(x1, y1), B(x2, y2), C(x3, y3) are three points in coordinate plane, then
d(A, B) + d(B, C) ≥ d(A, C) i.e. AB + BC ≥ AC.
If, A, B, C are collinear points and A—B—C then, AB + BC = AC.
If, A, B, C are non-collinear points or collinear but B—A—C or A—C—B, then AB + BC > AC
The formula for PQ can also be written as PQ2 = (x1-x2)2 + (y1-y2)2. While solving the examples, this form of distance formula is advantageous. We have to be careful that at the end when we find the distance ‘PQ’ we have to take the positive square root of the expression for PQ2.
Read more: Section Formula
Distance Between Two Points With Examples
Example 1: Find the distance between two points
(i) P(–6, 7) and Q(–1, –5)
(ii) R(a + b, a – b) and S(a – b, –a – b)
\(\left( \text{iii} \right)\text{ A(at}_{1}^{2}\text{, 2a}{{\text{t}}_{1}}\text{) and B(at}_{2}^{2}\text{, 2a}{{\text{t}}_{2}}\text{)}\)
Sol. (i) Here, x1 = – 6, y1 = 7 and x2 = – 1, y2 = – 5
∴ \( PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} \)
\( \Rightarrow PQ=\sqrt{{{(-1+6)}^{2}}+{{(-5-7)}^{2}}} \\ \)
\( \Rightarrow PQ=\sqrt{25+144}=\sqrt{169}=13 \)
(ii) We have,
\( RS=\sqrt{{{(a-b-a-b)}^{2}}+{{(-a-b-a+b)}^{2}}} \)
\( \Rightarrow RS=\sqrt{4{{b}^{2}}+4{{a}^{2}}}=2\sqrt{{{a}^{2}}+{{b}^{2}}} \)
(iii) We have,
\( AB=\sqrt{{{(a{{t}_{2}}^{2}-a{{t}_{1}}^{2})}^{2}}+{{(2a{{t}_{2}}-2a{{t}_{1}})}^{2}}} \)
\( \Rightarrow AB=\sqrt{{{a}^{2}}{{({{t}_{2}}-{{t}_{1}})}^{2}}{{({{t}_{2}}+{{t}_{1}})}^{2}}+4{{a}^{2}}{{({{t}_{2}}-{{t}_{1}})}^{2}}} \)
\(\Rightarrow AB=a({{t}_{2}}-{{t}_{1}})\sqrt{{{({{t}_{2}}+{{t}_{1}})}^{2}}+4}\)
Example 2: If the point (x, y) is equidistant from the points (a + b, b – a) and (a – b, a + b), prove that bx = ay.
Sol. Let P(x, y), Q(a + b, b – a) and R (a – b, a + b) be the given points. Then
PQ = PR (Given)
\(\Rightarrow \sqrt{{{\{x-(a+b)\}}^{2}}+{{\{y-(b-a)\}}^{2}}}=\sqrt{{{\{x-(a-b)\}}^{2}}+{{\{y-(a+b)\}}^{2}}}\)
⇒ {x – (a + b)}2 + {y – (b – a)}2 = {x – (a – b)}2 + {y – (a + b)}2
⇒ x2 – 2x (a + b) + (a + b)2 + y2 – 2y (b – a) + (b – a)2 = x2 + (a – b)2 – 2x(a – b) + y2 – 2 (a + b) + (a + b)2
⇒ –2x (a + b) – 2y (b – a) = – 2x (a – b) – 2y (a + b)
⇒ ax + bx + by – ay = ax – bx + ay + by
⇒ 2bx = 2ay ⇒ bx = ay
Example 3: Find the value of x, if the distance between the points (x, – 1) and (3, 2) is 5.
Sol. Let P(x, – 1) and Q(3, 2) be the given points, Then,
PQ = 5 (Given)
\(\Rightarrow \sqrt{{{(x-3)}^{2}}+{{(-1-2)}^{2}}}=5\)
⇒ (x – 3)2 + 9 = 52
⇒ x2 – 6x + 18 = 25 ⇒ x2 – 6x – 7 = 0
⇒ (x – 7) (x + 1) = 0 ⇒ x = 7 or x = – 1
Example 4: Show that the points (a, a), (–a, –a) and (– √3 a, √3 a) are the vertices of an equilateral triangle. Also find its area.
Sol. Let A (a, a), B(–a, –a) and C(– √3 a, √3 a) be the given points. Then, we have
\( AB=\sqrt{{{(-a-a)}^{2}}+{{(-a-a)}^{2}}}=\sqrt{4{{a}^{2}}+4{{a}^{2}}}=2\sqrt{2}a \)
\( BC=\sqrt{{{(-\sqrt{3}a+a)}^{2}}+{{(\sqrt{3}a+a)}^{2}}} \)
\( \Rightarrow BC=\sqrt{{{a}^{2}}{{(1-\sqrt{3})}^{2}}+{{a}^{2}}{{(\sqrt{3}+1)}^{2}}} \)
\( \Rightarrow BC=a\sqrt{1+3-2\sqrt{3}+1+3+2\sqrt{3}}=a\sqrt{8}=2\sqrt{2}a \)
\( and,\text{ }AC=\sqrt{(-\sqrt{3}a-{{a}^{2}})+{{(\sqrt{3}a-a)}^{2}}} \\ \)
\( \Rightarrow AC=\sqrt{{{a}^{2}}(\sqrt{3}+1)+{{a}^{2}}{{(\sqrt{3}-1)}^{2}}} \)
\( \Rightarrow AC=\sqrt{3+1+2\sqrt{3}+3+1-2\sqrt{3}}=a\sqrt{8}=2\sqrt{2}a \)
Clearly, we have
AB = BC = AC
Hence, the triangle ABC formed by the given points is an equilateral triangle.
Now,
Area of ∆ABC = \(\frac { \sqrt { 3 } }{ 4 } \) (side)2
⇒ Area of ∆ABC = \(\frac { \sqrt { 3 } }{ 4 } \) × AB2
⇒ Area of ∆ABC = \(\frac { \sqrt { 3 } }{ 4 } \) × (2√2 a)2 sq. units = 2√3 a2 sq. units
Example 5: Show that the points (1, – 1), (5, 2) and (9, 5) are collinear.
Sol. Let A (1, –1), B (5, 2) and C (9, 5) be the given points. Then, we have Clearly, AC = AB + BC
\( AB=\sqrt{{{(5-1)}^{2}}+{{(2+1)}^{2}}}=\sqrt{16+9}=5 \)
\( BC=\sqrt{{{(5-9)}^{2}}+{{(2-5)}^{2}}}=\sqrt{16+9}=5 \)
\( and,~~~~~AC=\sqrt{{{(1-9)}^{2}}+{{(-1-5)}^{2}}}=\sqrt{64+36}=10 \)
Hence, A, B, C are collinear points.
Example 6: Show that four points (0, – 1), (6, 7), (–2, 3) and (8, 3) are the vertices of a rectangle. Also, find its area.
Sol. Let A (0, –1), B(6, 7), C(–2, 3) and D (8, 3) be the given points. Then,
\( AD=\sqrt{{{(8-0)}^{2}}+{{(3+1)}^{2}}}=\sqrt{64+16}=4\sqrt{5} \)
\( BC=\sqrt{{{(6+2)}^{2}}+{{(7-3)}^{2}}}=\sqrt{64+16}=4\sqrt{5} \)
\( AC=\sqrt{{{(-2-0)}^{2}}+{{(3+1)}^{2}}}=\sqrt{4+16}=2\sqrt{5} \)
\( and,\text{ }BD\text{ }=\sqrt{{{(8-6)}^{2}}+{{(3-7)}^{2}}}=\sqrt{4+16}=2\sqrt{5} \)
∴ AD = BC and AC = BD.
So, ADBC is a parallelogram,

\( Now,\text{ }AB\text{ }=\sqrt{{{(6-0)}^{2}}+{{(7+1)}^{2}}}=\sqrt{36+64}=10 \)
\( and~~~~~~CD\text{ }=\sqrt{{{(8+2)}^{2}}+{{(3-3)}^{2}}}=10 \)
Clearly, AB2 = AD2 + DB2 and CD2 = CB2 + BD2
Hence, ADBC is a rectangle.
Now, Area of rectangle ADBC = AD × DB
= (4√5 × 2√5 ) sq. units = 40 sq. units
Example 7: If P and Q are two points whose coordinates are (at2, 2at) and (a/t2, 2a/t) respectively and S is the point (a, 0). Show that \(\frac{1}{SP}+\frac{1}{SQ}\) is independent of t.
Sol. We have,
\( SP=\sqrt{{{(a{{t}^{2}}-a)}^{2}}+{{(2at-0)}^{2}}} \)
\( =\sqrt{{{({{t}^{2}}-1)}^{2}}+4{{t}^{2}}}=a({{t}^{2}}+\text{ }1) \)
\( and~~~~~~SQ\text{ }=\sqrt{{{\left( \frac{a}{{{t}^{2}}}-a \right)}^{2}}+{{\left( \frac{2a}{t}-0 \right)}^{2}}} \)
\( \Rightarrow SQ\text{ }=\sqrt{\frac{{{a}^{2}}{{(1-{{t}^{2}})}^{2}}}{{{t}^{4}}}+\frac{4{{a}^{2}}}{{{t}^{2}}}} \)
\( \Rightarrow SQ\text{ }=\frac{a}{{{t}^{2}}}\sqrt{{{(1-{{t}^{2}})}^{2}}+4{{t}^{2}}}=\frac{a}{{{t}^{2}}}\sqrt{{{(1+{{t}^{2}})}^{2}}} \)
which is independent of t.
\( =~\frac{a}{{{t}^{2}}}(1\text{ }+\text{ }{{t}^{2}})~ \)
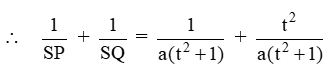
\( \Rightarrow \frac{1}{SP}+\frac{1}{SQ}=\frac{1+{{t}^{2}}}{a({{t}^{2}}+1)}=\frac{1}{a} \)
Example 8: If two vertices of an equilateral triangle be (0, 0), (3, √3 ), find the third vertex.
Sol. O(0, 0) and A(3, √3) be the given points and let B(x, y) be the third vertex of equilateral ∆OAB. Then, OA = OB = AB
⇒ OA2 = OB2 = AB2
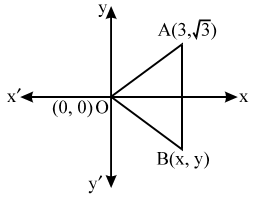
We have, OA2 = (3 – 0)2 + (√3 – 0)2 = 12,
OB2 = x2 + y2
and, AB2 = (x – 3)2+ (y – √3)2
⇒ AB2 = x2 + y2 – 6x – 2 y + 12
∴ OA2 = OB2 = AB2
⇒ OA2 = OB2 and OB2 = AB2
⇒ x2 + y2 = 12
and, x2 + y2 = x2 + y2 – 6x – 2 √3y + 12
⇒ x2 + y2 = 12 and 6x + 2 √3y = 12
⇒ x2 + y2 = 12 and 3x + √3y = 6
\( \Rightarrow \text{ }~{{x}^{2}}~+\text{ }{{\left( \frac{6-3x}{\sqrt{3}} \right)}^{2}}=\text{ }12\text{ }\left[ \because \ 3x+\sqrt{3}y=6\ \ \therefore \ \ y=\frac{6-3x}{\sqrt{3}} \right] \)
⇒ 3x2 + (6 – 3x)2 = 36
⇒ 12x2 – 36x = 0 ⇒ x = 0, 3
∴ x = 0 ⇒ √3y = 6
\( \Rightarrow \text{ }y=\frac{6}{\sqrt{3}}=2\sqrt{3}\text{ }\left[ \text{Putting}\ \text{x}=\text{0}\ \text{in 3x + }\sqrt{\text{3}}\text{y}=\text{6} \right] \)
and, x = 3 ⇒ 9 + √3 y = 6
\(\Rightarrow \text{ }y=\frac{6-9}{\sqrt{3}}=-\sqrt{3}\text{ }\left[ \text{Putting}\ \text{x}=\text{0}\ \text{in 3x + }\sqrt{\text{3}}\text{y}=\text{6} \right]\)
Hence, the coordinates of the third vertex B are (0, 2 √3) or (3, – √3).
Example 9: Find the coordinates of the circumcentre of the triangle whose vertices are (8, 6), (8, – 2) and (2, – 2). Also, find its circum radius.
Sol. Recall that the circumcentre of a triangle is equidistant from the vertices of a triangle. Let A (8, 6), B(8, –2) and C(2, – 2) be the vertices of the given triangle and let P (x, y) be the circumcentre of this triangle. Then,
PA = PB = PC ⇒ PA2 = PB2 = PC2
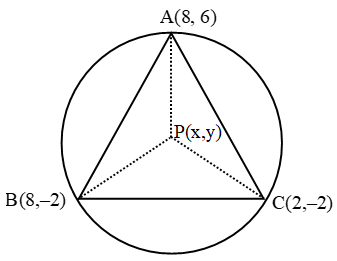
Now, PA2 = PB2
⇒ (x – 8)2 + (y – 6)2 = (x – 8)2 + (y + 2)2
⇒ x2 + y2 – 16x – 12y + 100 = x2 + y2 – 16x + 4y + 68
⇒ 16y = 32 ⇒ y = 2
and, PB2 = PC2
⇒ (x – 8)2 + (y + 2)2 = (x – 2)2 + (y + 2)2
⇒ x2 + y2 – 16x + 4y + 68 = x2 + y2 – 4x + 4y + 8
⇒ 12x = 60 ⇒ x = 5
So, the coordinates of the circumcentre P are (5, 2).
Also, Circum-radius = PA = PB = PC
\(=\sqrt{{{(5-8)}^{2}}+{{(2-6)}^{2}}}=\sqrt{9+16}=5\)
Example 10: If the opposite vertices of a square are (1, – 1) and (3, 4), find the coordinates of the remaining angular points.
Sol. Let A(1, – 1) and C(3, 4) be the two opposite vertices of a square ABCD and let B(x, y) be the third vertex.
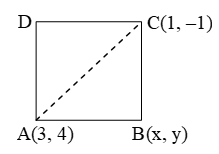
Then, AB = BC
⇒ AB2 = BC2
⇒ (x – 1)2 + (y + 1)2 = (3 – x)2 + (4 – y)2
⇒ x2 – 2x + 1 + y2 + 2y + 1 = 9 – 6x + x2 + 16 – 8y + y2
⇒ x2 + y2 – 2x + 2y + 2 = x2 + y2 – 6x – 8y + 25
⇒ 4x + 10y = 23
⇒ x = \(\frac { 23-10y }{ 4 }\) ….(1)
In right-angled triangle ABC, we have
AB2 + BC2 = AC2
⇒ (x – 3)2 + (y – 4)2 + (x – 1)2 + (y + 1)2 = (3 –1)2 + (4 + 1)2
⇒ x2 + y2 – 4x – 3y – 1 = 0 …. (2)
Substituting the value of x from (1) and (2),
we get
\({{\left( \frac{23-10y}{4} \right)}^{2}}\)+ y2 – (23 – 10y) – 3y – 1 = 0
⇒ 4y2 – 12y + 5 = 0 ⇒ (2y – 1) (2y – 5) = 0
⇒ y = \(\frac { 1 }{ 2 }\) or \(\frac { 5 }{ 2 }\)
Putting y = \(\frac { 1 }{ 2 }\) and y = \(\frac { 5 }{ 2 }\)respectively in (1) we get
x = \(\frac { 9 }{ 2 }\) and x = \(\frac { -1 }{ 2 }\) respectively.
Hence, the required vertices of the square are \(\left( \frac{9}{2},\ \frac{1}{2} \right)\text{ and }\left( -\frac{1}{2},\ \frac{5}{2} \right) \).
Example 11: Prove that the points (–3, 0), (1, –3) and (4, 1) are the vertices of an isosceles right angled triangle. Find the area of this triangle.
Sol. Let A (–3, 0), B (1, –3) and C (4, 1) be the given points. Then,
\( AB=\sqrt{{{\{1-(-3)\}}^{2}}+{{(-3-0)}^{2}}}=\sqrt{16+9}=5\text{ }units. \)
\( BC=\sqrt{{{(4-1)}^{2}}+{{(1+3)}^{2}}}=\sqrt{9+16}=5\text{ }units. \)
\( CA=\sqrt{{{(4+3)}^{2}}+{{(1-0)}^{2}}}=\sqrt{49+1}=5\sqrt{2}\text{ }units. \)
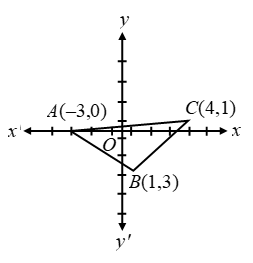
Clearly, AB = BC. Therefore, ∆ABC is isosceles.
Also, AB2 + BC2 = 25 + 25 = (5)2 = CA2
⇒ ∆ABC is right-angled at B.
Thus, ∆ABC is a right-angled isosceles triangle.
Now, Area of ∆ABC = \(\frac { 1 }{ 2 }\) (Base × Height)
= \(\frac { 1 }{ 2 }\) (AB × BC)
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) × 5 × 5 sq. units
= \(\frac { 25 }{ 2 }\) sq. units.
Example 12: If P (2, – 1), Q(3, 4), R(–2, 3) and S(–3, –2) be four points in a plane, show that PQRS is a rhombus but not a square. Find the area of the rhombus.
Sol. The given points are P(2, –1), Q(3, 4), R(–2, 3) and S(–3, –2).
We have,
\( PQ=\sqrt{{{(3-2)}^{2}}+{{(4+1)}^{2}}}=\sqrt{{{1}^{2}}+{{5}^{2}}}=\sqrt{26}\text{ }units \)
\( QR=\sqrt{{{(-2-3)}^{2}}+{{(3-4)}^{2}}}=\sqrt{25+1}=\sqrt{26}\text{ }units \)
\( RS=\sqrt{{{(-3+2)}^{2}}+{{(-2-3)}^{2}}}=\sqrt{1+25}=\sqrt{26}\text{ }units \)
\( SP=\sqrt{{{(-3-2)}^{2}}+{{(-2+1)}^{2}}}=\sqrt{25+1}=\sqrt{26}\text{ }units \)
\( PR=\sqrt{{{(-2-2)}^{2}}+{{(3+1)}^{2}}}=\sqrt{16+16}=4\sqrt{2}\text{ }units \)
\( QS=\sqrt{{{(-3-3)}^{2}}+{{(-2-4)}^{2}}}=\sqrt{36+36}=6\sqrt{2}\text{ }units \)
∴ PQ = QR = RS = SP = units
and, PR ≠ QS
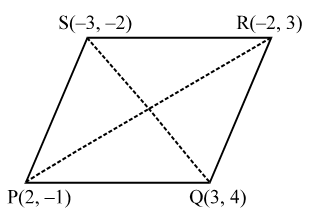
This means that PQRS is a quadrilateral whose sides are equal but diagonals are not equal.
Thus, PQRS is a rhombus but not a square.
Now, Area of rhombus PQRS = \(\frac { 1 }{ 2 }\) × (Product of lengths of diagonals)
⇒ Area of rhombus PQRS = \(\frac { 1 }{ 2 }\) × (PR × QS)
⇒ Area of rhombus PQRS
\(=\left( \frac{1}{2}\times 4\sqrt{2}\times 6\sqrt{2} \right)sq.\text{ }units\text{ }=\text{ }24\text{ }sq.\text{ }units\)
Example 13: Find the coordinates of the centre of the circle passing through the points (0, 0), (–2, 1) and (–3, 2). Also, find its radius.
Sol. Let P (x, y) be the centre of the circle passing through the points O(0, 0), A(–2,1) and B(–3,2).
Then, OP = AP = BP
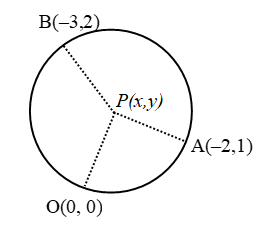
Now, OP = AP ⇒ OP2 = AP2
⇒ x2 + y2 = (x + 2)2 + (y – 1)2
⇒ x2 + y2 = x2 + y2 + 4x – 2y + 5
⇒ 4x – 2y + 5 = 0 ….(1)
and, OP = BP ⇒ OP2 = BP2
⇒ x2 + y2 = (x + 3)2 + (y – 2)2
⇒ x2 + y2 = x2 + y2 + 6x – 4y + 13
⇒ 6x – 4y + 13 = 0 ….(2)
On solving equations (1) and (2), we get
x = \(\frac { 3 }{ 2 }\) and y = \(\frac { 11 }{ 2 }\)
Thus, the coordinates of the centre are \( \left( \frac{3}{2},\ \frac{11}{2} \right) \)
\(Now,\text{ }Radius=OP=\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{\frac{9}{4}+\frac{121}{4}} \)
\( =\frac{1}{2}\sqrt{130}\text{ }units. \)