What are the Different Kinds of Quadrilateral

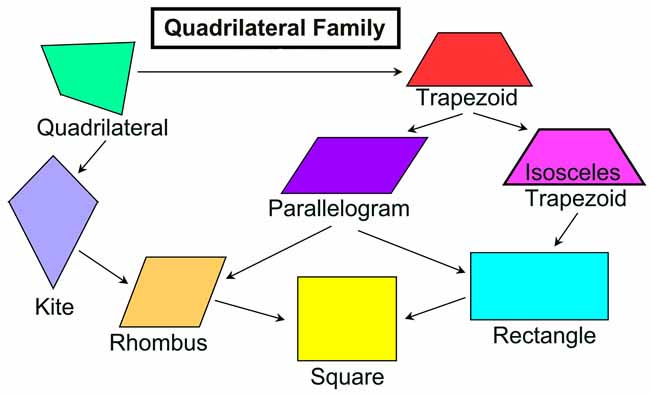
Different Types of Quadrilaterals

Quadrilaterals are categorised as the following, depending upon their sides.

• Parallelogram
• Rhombus
• Rectangle
• Square
• Trapezium
• Isosceles Trapezium
• Kite

• More Solved examples on Quadrilaterals
• Properties of Cyclic Quadrilaterals
• RS Aggarwal Class 9 Solutions Quadrilaterals and Parallelograms

Parallelogram: A quadrilateral in which the pairs of opposite sides are parallel, is called a parallelogram.
 In a parallelogram,

1. Opposite sides are equal and parallel, i.e., AB = DC, BC = AD, AB || DC, and BC || AD.
2. Opposite angles are equal, i.e., ∠A = ∠C and ∠B = ∠D.
3. Diagonals bisect each other, i.e., AO = OC and BO = OD.
4. Diagonal divides the parallelogram into two congruent triangles, i.e., ΔADC and ΔABC are congruent and ΔADB and ΔCBD are congruent.

Rectangle: A parallelogram in which each angle is a right angle, is called a rectangle.
In a rectangle,

1. Opposite sides are equal and parallel, i. e., AB = CD, AB || CD, BC = DA, and BC || DA.
2. All angles are right angles, i.e., ∠A = ∠B = ∠C = ∠D = 90°.
3. Both the diagonals are equal, i.e., AC = BD.
4. Diagonals bisect each other, i.e., AR = RC and BR = RD.

Rhombus: A parallelogram in which all four sides are equal, is called a rhombus.
In a rhombus,

1. All sides are equal, i.e., PQ = QR = RS = SR
2. Opposite sides are parallel, i.e., PQ || SR and SP || RQ.
3. Opposite angles are equal, i.e., ∠P = ∠R and ∠Q = ∠S
4. Diagonals bisect each other at right angle, i.e., PO = OR, SO = OQ and ∠SOR = ∠SOP = ∠ROQ = ∠QOP = 90°.

Square: A rhombus with all its angles equal to right angle, is called a square.
In other words, a square is a rectangle in which all the four sides are equal.
In a square,

1. Opposite sides are parallel, i.e., AB || DC and AD || BC.
2. All the sides are equal, i.e.,  AB = BC = CD = DA.
3. All the angles are equal to 90°, i.e., ∠A = ∠B = ∠C = ∠D = 90°
4. The diagonals bisect each other at right angle,
   i. e., AO = OC and BO = OD and ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
5. Both the diagonals are equal in length, i.e., AC = BD.

Trapezium: A quadrilateral in which one pair of opposite sides are parallel, is called a trapezium.
In a trapezium,

1. A pair of opposite sides is parallel.
2. Both the diagonals AC and BD are of different lengths.
3. Diagonals do not bisect each other at right angle.
4. Opposite angles are not equal.

Isosceles trapezium: A quadrilateral in which a pair of opposite sides is parallel and the other two sides are equal, is called an isosceles trapezium.
In an isosceles trapezium,

1. A pair of opposite sides is parallel, i.e., AB || CD.
2. Non-parallel sides are equal, i.e., AD = BC.
3. Both the diagonals are equal, i.e., AC = BD.
4. ∠A = ∠B and ∠D = ∠C.

Kite: A quadrilateral in which two pairs of adjacent sides are equal is called a kite.
In a kite,

1. Two pairs of adjacent sides are equal, i.e., AB = AD and BC = CD.
2. Diagonals intersect each other at right angle, i.e., ∠AEB = ∠AED = ∠BEC = ∠DEC = 90°.